Читайте также:
|
Ранее было показано, что частотные характеристики цифровых систем в области низких частот для значений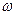 
<2/T практически совпадают с частотными характеристиками непрерывной части разомкнутой системы. Это оказывается справедливым для цифровых систем при линеаризации задачи и в предположении, что передаточная функция самой цифровой части D(z)=1 или в общем случае D(z)=h=const.
Кроме того, следует заметить, что для обеспечения необходимого запаса устойчивости приходится всегда выбирать желаемую ЛАХ, чтобы удовлетворялось условие 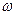cp<2/T, где 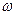cp- частота среза. Поэтому на импульсные и цифровые системы можно распространить правила построения запретной области для ЛАХ, рассмотренные ранее. На рисунке показано построение запретной области ЛАХ в случае использования астатической системы регулирования.
Эта область построена в функции псевдочастоты l=2/T tg(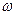 T/2). Для частот меньших чем частота среза l<lcp псевдочастота практически совпадает с обычной круговой частотой l» .
 | |||
| |||
| |||
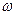Частота контрольной точки Aк опеделяется формулой lg=amax/Wmax, где amax и Wmax максимальные значения скорости и ускорения воздействия g(t) на входе.
Базовая частота
Ka- добротность по ускорению
emax- максимально допустимое значение ошибки.
Дата добавления: 2015-07-20; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Построение низкочастотной части ЛЧХ | | | Расчет дискретных корректирующих средств. |