Гидродинамические модели реакторов.

Модель идеального вытеснения.

Реактор вытеснения представляет собой аппарат непрерывного действия, в котором не предусматривается перемешивания среды в каких либо точках по направлению потока.

Под режимом идеального вытеснения понимается идеализированное состояние потока, которое характеризуется следующими свойствами:

1. В любом поперечном сечении, нормальном к движению жидкости скорость и свойства среды (температура, давление, концентрации реагентов и продуктов реакции) постоянны.

2. Диффузия пренебрежимо мала по сравнению с линейной скоростью потока.

3. Движущийся поток имеет линейный профиль скоростей.

Первое условие означает, что все элементы среды проходят через реактор за одинаковое время и претерпевают одну и ту же последовательность изменений всех параметров процесса.

Второе условие означает, что молекулы реагентов и продуктов не диффундируют из одного элементарного объёма в другой при прохождении через реактор. Отсюда следует, что в каждом элементе, расположенном по длине реактора, степень превращения является одной и той же и поэтому эти элементы можно рассматривать, как миниатюрные реакторы периодического действия, перемещающиеся вдоль оси реактора.

Таким образом, реактор вытеснения в целом можно характеризовать теми же параметрами, что и систему периодического действия с длительностью реакции, равной времени прохождения элемента через реактор вытеснения.

Предположим, что в реакторе не содержится ни твёрдого катализатора, ни насадки. Пусть P и Q две плоскости, ограничивающие бесконечно малый элементарный объём dVr, от общего объёма реактора. Пусть G – массовая скорость потока, через обе плоскости.

В условиях стационарного режима массовая скорость постоянна для всех таких плоскостей.

Пусть Y и Y + dY выражают число моль продукта, которые приходятся на единицу массы среды, соответственно в плоскостях P и Q.

В соответствии с моделью идеального вытеснения эти концентрации одинаковы по всему поперечному сечению, так же, как и скорость реакции и массовый расход среды.

Пусть символ r обозначает скорость реакции имеющую размерность - моль/литр _* мин.

Тогда уравнение баланса массы будет иметь вид:

G _* (Y + dY) = G _* Y + r dV_r

G dY = r dV_r – интегрируя это выражение, можно получить общий объём реактора, выраженный через концентрацию на выходе из реактора Ye.

Уравнение справедливо если концентрация продукта Y_i на входе в реактор равна 0. Если концентрация продукта Y_i, на входе в реактор на равна 0, а имеет конкретное значение, выражение примет вид:

В случае, если в реакторе находятся частицы катализатора, тогда скорость реакции, отнесённая к единицы массы катализатора (r^/); W_r – общая масса катализатора, необходимая для достижения на выходе из реактора концентрации Y_е

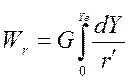или

В качестве примера возьмем газофазную, гомогенную реакцию между реагентами А и В. Для упрощения примем, что реакция необратима, а кинетическое уравнение имеет вид: r = K[A]^a[B]^b

В этом случае объёмные концентрации реагентов А и В могут быть достаточно легко выражены через переменную Y.

Это уравнение справедливо если:

1. Если сохраняется температура по всей длине реактора и по всему поперечному сечению, как это следует из модели идеального вытеснения. Требование постоянной температуры наиболее полно удовлетворяются при малых теплотах реакции. В других случаях постоянства температуры может быть достигнуто за счёт постоянства температуры стенки реактора (например, при помощи рубашки, при малом диаметре реактора, или за счёт высокой турбулизации потока, обеспечивающей эффективный отвод тепла из объёма среды к стенке).

2. Когда реакция протекает в адиабатическом реакторе то есть стенки реактора изолированы очень хорошо и потери тепла в направлении перпендикулярном потоку пренебрежимо малы. В этом случае температура будет возрастать или снижаться вдоль оси потока в зависимости от теплового эффекта реакции. При этом характер изменения температуры легко определяется по тепловому эффекту реакции.

Дата добавления: 2015-07-25