в стационарном режиме

При необходимости получения большого количества продукта одинакового качества химический процесс предпочитают проводить в непрерывно действующих реакторах работающих в стационарном режиме.

При составлении уравнения материального баланса для проточного реактора идеального смешения, работающего без рециркуляции из выражения можно исключить оператор, описывающий диффузионный перенос.

Кроме того, при стационарном режиме работы реактора из уравнения исключается производная dC/dt которая не равна 0 только при наличии накопления вещества в аппарате.

Таким образом остаются только два члена уравнения описывающие конвективный перенос вещества (вызванный движением жидкости) и член учитывающий протекание химической реакции.

Кроме того в проточном реакторе происходит не мгновенное, а дискретное изменение концентрации DС_J сразу же на входе в реактор. По этому можно заменить градиент концентрации на отношение конечного изменения концентрации DС_J к изменению координаты DZ при прохождении реакционного потока через аппарат со средней линейной скоростью 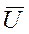, а среднюю линейную скорость потока через реактор заменить отношением объёмного расхода к площади поперечного сечения реактора:

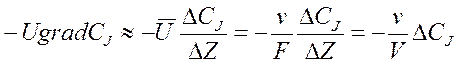, где

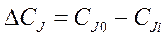(разность концентраций на входе и выходе из реактора)

Окончательно уравнение материального баланса примет вид:

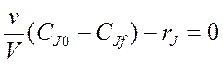или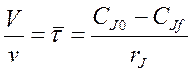

Величина измеряется в единицах времени и характеризует среднее время в течении которого обновляется содержание проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе. Действительное время пребывания является случайной величиной которое может изменяться от 0 до бесконечности и может быть задано при помощи вероятностных характеристик.

Использование характеристики среднее время пребывания является удобным способом усреднения действительного времени пребывания, так как эта величина связана конструктивными особенностями реактора, а именно его объёмом и объёмным расходом реакционной смеси.

Для решения практических задач концентрацию реагента C_Jf выражают через его степень превращения X_Jf.

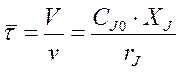
Уравнение материального баланса для проточного реактора идеального смешения работающего в стационарном режиме отличается от соответствующих уравнений для периодического реактора смешения. Они записаны сразу в алгебраической форме в отличие от дифференциальной формы для периодического реактора.

В уравнении для периодического реактора скорость химической реакции следует подставлять в виде функциональной зависимости от концентрации r_J=f(C_J) или от степени превращения r_J=f(Х_J) и только после интегрирования возможна подстановка числовых значений.

В проточном реакторе идеального смешения, работающим в стационарном режиме, в любой точке реактора в любой промежуток времени концентрация постоянна и, следовательно, характеризуется конкретным числовым значением. Это число может быть сразу подставлено в уравнение материального баланса.

Уравнение материального баланса для проточного реактора может быть использоваться не только для расчёта размеров реактора 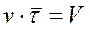при заданной глубине химического превращения, но и для решения обратной задачи, при заданном объёме реактора и заданной производительности по исходному реагенту определить его концентрацию на выходе из реактора если кинетика его превращения описывается простым уравнением первого или второго порядка. Так для реакции первого порядка А®R

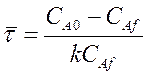отсюда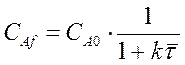

Если скорость сложной реакции описывается кинетическим уравнением дробного порядка, то аналитическое решение становится невозможным. В таких случаях пользуются аналитическими методами расчёта.

В качестве примера рассмотрим графический метод определения концентрации реагентов на выходе из проточного стационарного реактора идеального вытеснения.

Преобразуем уравнение материального баланса к виду:

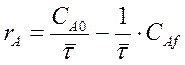
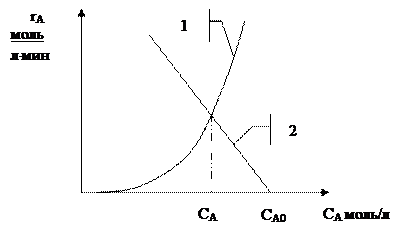
В левой части уравнения записана кинетическая зависимость скорости данной реакции. В соответствии с законом действующих масс скорость химической реакции пропорциональна концентрации реагентов, следовательно r_A =f (С_А) возрастающая функция, которая может быть представлена графически (кривая 1). Она пересекает ось абсцисс в точке, соответствующей равновесной концентрации для обратимых реакций или выходит из начала координат для необратимых реакций.

В правой части уравнения записана соответствующая уравнению материального баланса стационарного реактора идеального смешения линейная функция скорости реакции от концентрации исходного реагента. Эта функция имеет отрицательный угловой коэффициент 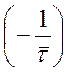. График этой линии – прямая, пересекающая ось концентраций в точке С_А0 (линия 2). Как видно, линии 1 и 2 пересекаются в единственной точке М. Абсцисса этой точки и есть искомая концентрация реагента на выходе из реактора идеального смешения.

Дата добавления: 2015-07-25