Уравнение материального баланса для РИВ

Уравнение материального баланса описывающее химический процесс в любом реакторе по произвольному участнику J для элементарного объёма проточного реактора и элементарного промежутка времени t имеет вид:

В этом уравнении первый член отражает перенос импульса (где U линейная скорость в направлении осей координат). Второй член уравнения учитывает диффузию (где D коэффициент диффузии, а Ñ (набла) оператор Лапласа .

Третий член уравнения учитывает непосредственное протекание химической реакции.

В соответствии с принятым допущением об идеальности реактора вытеснения (плоский профиль линейных скоростей, отсутствие перемешивания вдоль оси реактора, все параметры процесса, в каждом сечении, перпендикулярном оси потока – постоянны) общее уравнение материального баланса для элементарного объёма можно упростить.

В качестве элементарного объёма выберем объём вырезанный двумя параллельными плоскостями, расположенными на бесконечно малом расстоянии вдоль оси Z.

		U

Z Z+dZ

L

В соответствии с третьим допущением .

Следовательно, конвективный перенос происходит только в направлении оси Z.

В соответствии со вторым и третьим допущениями – диффузионный перенос отсутствует.

Тогда исходное уравнение для реактора идеального вытеснения, работающего в нестационарном режиме, будет иметь вид:

В случае стационарного режима, правая часть уравнения приравнивается к 0 и выражение записывается в виде:

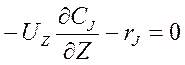
Для реактора с постоянной площадью поперечного сечения канала, линейная скорость потока U_Z будет величиной постоянной, равной отношению объёмного расхода v к площади поперечного сечения F (U_Z= v/ F). Исходя из того, что произведение F×Z=V есть объем реактора, а отношение (v/F×Z)=U, отношение уравнение материального баланса для реактора идеального вытеснения, работающего в стационарном режиме, можно привести к виду:

Среднее время пребывания реагентов в проточном реакторе характеризует продолжительность прохождения потоком расстояния от входа в реактор до некоторой точки Z на оси реактора.

Для стационарного режима идеального вытеснения уравнение материального баланса можно проинтегрировать относительно :

или, если J исходный реагент:

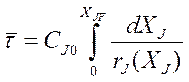
Полученные уравнения могут быть использованы для расчётов реактора идеального вытеснения, работающего в изотермическом режиме, а так же глубины протекающих в нем процессов.

Дата добавления: 2015-07-25