Алгоритм вычисления показателей в динамической модели и экономический анализ полученных результатов

Вычисления производим, используя табличный редактор «Excel».

1. Необходимо создать матрицу технологических коэффициентов a_ij с суммой по столбцам и строкам не более 0,6, взяв за основу исходные данные:

A =	0,1	0,1		0,02	0,04
0,15	0,05		0,1	0,1
0,05	0,1	0,2	0,14	0,1
0,15	0,15	0,1	0,04	0,18
0,05	0,1	0,2		0,16

2. Далее создадим матрицу приростной фондоемкости по принципу: 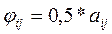, получим:

jij =	0,05	0,05		0,01	0,02
0,075	0,025		0,05	0,05
0,025	0,05	0,1	0,07	0,05
0,075	0,075	0,05	0,02	0,09
0,025	0,05	0,1		0,08

3. На основе двух полученных матриц создать матрицу из элементов вида: 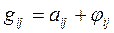, получим:

gij =	0,15	0,15		0,03	0,06
0,225	0,075		0,15	0,15
0,075	0,15	0,3	0,21	0,15
0,225	0,225	0,15	0,06	0,27
0,075	0,15	0,3		0,24

Необходимо вычислить суммы элементов по строкам и столбцам для проверки выполнения условия, что они не превышают единицы. В данном варианте эти условия выполняются.

Предполагается, что производственные мощности используются полностью и прирост продукции равен приросту мощности.

4. На основе матрицы, состоящей из элементов a_ij, создадим преобразованную матрицу вида:

(E – A) =	0,9	-0,1		-0,02	-0,04
-0,15	0,95		-0,1	-0,1
-0,05	-0,1	0,8	-0,14	-0,1
-0,15	-0,15	-0,1	0,96	-0,18
-0,05	-0,1	-0,2		0,84

5. Зададимся законами изменения конечных продуктов Y’_i (t), взяв за Y’_i (t₀) значение из заданного варианта. Каждое последующее значение Y’_i (t) необходимо взять на 40% больше предыдущего. Время возьмем в пределах 0, 1, 2, 3, 4, получим:

	t0	t1	t2	t3	t4
Y1					1920,8
Y2					3841,6
Y3					7683,2
Y4					13445,6
Y5				2881,2	4033,68

6. На основе преобразованной матрицы технологических коэффициентов, полученной при выполнении 4 этапа, и Y’_I (t₀) рассчитать исходные валовые выпуски X_i (t₀). Получим:

X5	X4	X3	X2	X1

7. Рассчитаем значения величин Y_i’^(t) для t = 1 по формуле:

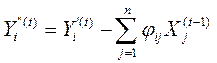
(1)

Получим:

y'i(t=1)

8. На основе матрицы, состоящей из элементов g_ij, создать преобразованную матрицу вида:

(E – gij) =	0,85	-0,15		-0,03	-0,06
-0,225	0,925		-0,15	-0,15
-0,075	-0,15	0,7	-0,21	-0,15
-0,225	-0,225	-0,15	0,94	-0,27
-0,075	-0,15	-0,3		0,76

9. Взяв результаты 7 и 8 этапов как исходные данные, определим валовые выпуски для первого года X_i(t₁):

X5	X4	X3	X2	X1
4551,388	8062,799	6889,951	3442,427	1742,743

10. Рассчитаем значения величин Y_i’^(t) для t = 2 по формуле (1):

y'i(t=2)

549,0857

1112,524

2223,35

5555,734

789,2039

11. Взяв результаты 8 и 10 этапов как исходные данные, определим валовые выпуски для второго года X_i(t₂):

X5	X4	X3	X2	X1
5514,481	10423,87	8641,336	4313,803	2164,401

12. Рассчитаем значения величин Y_i’^(t) для t = 3 по формуле (1):

y'i(t=3)

833,5615

1676,907

3348,671

7981,287

1306,108

13. Взяв результаты 8 и 12 этапов как исходные данные, определим валовые выпуски для третьего года X_i(t₃):

X5	X4	X3	X2	X1
8402,836	15283,21	12898,62	6444,509	3250,476

14. Рассчитаем значения величин Y_i’^(t) для t = 4 по формуле (1):

y'i(t=4)

1115,162

2252,399

4499,884

11011,63

1668,104

15. Взяв результаты 8 и 14 этапов как исходные данные, определим валовые выпуски для четвертого года X_i(t₄):

X5	X4	X3	X2	X1
11219,52	20846,15	17419,23	8699,001	4374,786

16. Далее необходимо построить отдельно графики функций: Y_i’(t); X_i(t), а также графики функций Y’(t); X(t) для каждой отрасли (Приложения 1, 2, 3, 4, 5, 6,7).

Таблица 10

x1		1742,743	2164,401	3250,476	4374,786
x2		3442,427	4313,803	6444,509	8699,001
x3		6889,951	8641,336	12898,62	17419,23
x4		8062,799	10423,87	15283,21	20846,15
x5		4551,388	5514,481	8402,836	11219,52
y’1					1920,8
y’2					3841,6
y’3					7683,2
y’4					13445,6
y’5				2881,2	4033,68

Заключение

Межотраслевая модель «затраты – выпуск» (статическая модель Леонтьева). Сущность рассмотренного метода заключается в определении валового выпуска отрасли по заданному конечному спросу на основе данных о технологических возможностях, воплощенных в расходных коэффициентах a_ij. Может быть решена и обратная задача: по заданным валовым выпускам определяется объем конечного спроса на каждый продукт, т.е. Y_i.

Однако при рассмотрении данной модели необходимо помнить об имеющихся недостатках:

- новые капитальные вложения на оборудование не выделяется и любое расширение производства осуществляется за счет существующих мощностей;

- производятся новые капитальные вложения, но они представляют собой элементы конечного потребления;

- технические коэффициенты затрат постоянны и не изменяются с расширением производства, т.е. не являются ни функцией объема производства, ни функцией времени.

Динамическая межотраслевая балансовая модель. В рассмотренной динамической модели межотраслевого баланса предполагается, что прирост продукции текущего периода обуслов­лен капиталовложениями, произведенными в этом же периоде. Для сравнительно коротких периодов это предположение может оказаться нереальным, т.к. существуют известные, иногда довольно значитель­ные, отставания во времени (так называемые временные лаги) между вложением средств в производственные фонды и приростом выпуска продукции. Модели, так или иначе учитывающие лаг капитальных вложений, образуют особую группу динамических моделей межот­раслевого баланса. Из теоретических моделей данного типа выделяет­ся линейная динамическая межотраслевая модель Леонтьева, в кото­рой капитальные вложения представлены в виде так называемого ин­вестиционного блока в форме Леонтьева.

Список используемой литературы

1. Колемаев В. А., Математическая экономика: учебник для вузов. -Москва, 2002.

2. Пучков В. Ф., Математические модели макроэкономики: учеб. пособие.- 3 изд. перераб. и доп. – Гатчина: Изд-во ГИЭФПТ, 2010.

Дата добавления: 2015-07-25