Применение критерия Найквиста при наличии астатических и консервативных звеньев.

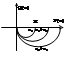Астатическое звено:W(p)=K_и/p, можно представить как предельный случай 1-го порядка т.е = lim_α→0K_и/(p+α)= (K_и/α)/(1/2*p+1)=K/T_p+1, α→0, K= K_и/α→∞. T=1/α. Тогда можно считать что АФХ

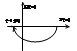
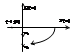астатического звена начин. на вещественной полуоси в бесконеч. и по дуге бесконеч. радиуса замык. на мнимой оси. т.е рис№2. Видно что АФХ не охватывает т. (-1;j0). Замкнутая САУ будет устойчивой. Пусть разом. система содержит 2 интегратора. W_p(p)=(K_и1/p)+(K_и2/p) => W_p(jω)=(K_и1*K_и2)/jω=- K_и1*K_и2/ω². Видим(рис№3) что при любых знач. параметра K_и1 и K_и2 замкнутая САУ будет наход. на гран. уст-ти. Услов. нахожден. системы на гр. устойчивости W(jω)=-1 можно разбить {^P(ω)=-1_Q(ω)=0,

-K_и1*K_и2/ω²=-1, ω= K_и1*K_и2. Рассмотрим 3 интегратора:

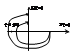W_p(p)=K₁*K₂*K₃*K_д/p³

АФХ раз. системы охват. т(-1;j0), замкн. САУ будет не устойчива при любых знач. параметров K₁,K₂,K₃, K_д. Системы которые

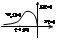будут не устойчивы при любых знач-ях параметров элементов назыв. структ. неусточивыми.

Систему можно устойчивой если преобразовать ее. Например охватив интегратор линейной обратной связью W_э(p)=(K_и/p)/(1+(K_и*K_α/p))=

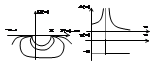K_и/(р+K_и*K_α)=(1/K_α)/((1/K_иK_α*р)+1). Консервативно колебательное звено: W(p)=K/T²p²+1= lim_ρ→0K/T²p²+2ρTp+1.

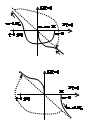W_p(p)=K/(T₁p+1)³(T₂² p²+1), T₁>T₂.

W_p(p)=K/(T₁p+1)(T₂² p²+1).

Дата добавления: 2015-07-25