Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Влияние запаздывания на устойчивость САУ.

Понятие о звене САУ и его статической характеристике. | Типовые входные воздействия. Переходная и импульсная характеристики. | Понятие передаточной функции. Свойства преобразования Лапласа. | Понятие о частотных характеристиках. | Типовые динамические звенья (временные и частотные характеристики, передаточные функции). | Преобразование структурных схем САУ. Связь структурных схем с графами. | Передаточные функции группы звеньев при последовательном, параллельном и встречно-параллельном соединении звеньев. | Понятие устойчивости САУ. | Связь устойчивости с корнями характеристического уравнения САУ. Теоремы Ляпунова. | Алгебраические критерии устойчивости(Рауса, Гурвица и т.д) |


Читайте также:
  1. III. Влияние гласных второго ряда на впереди стоящие согласные.
  2. А. Кислотоустойчивость
  3. А.Ф. Лосев Атеизм, его происхождение и влияние на науку и жизнь
  4. Алкоголизм, обусловленный влиянием среды и семьи
  5. Билет №35. Функции потребления и сбережения. Предельная склонность к потреблению и предельная склонность к сбережению, их взаимосвязь и влияние на «эффективный спрос».
  6. Богу угодно, чтобы церковь оказывала свое влияние
  7. В конечном итоге, удовлетворение потребителей оказывает влияние на акционерную ценность

Пусть имеем или можем выделить в системе звено чистого запаздывания

Проанализируем влияние запаздывания

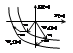на устойчивость системы после замыкания обратной связи. Используя критерий Найквиста Wp(p)= W1(p)×e-tp. КЧХ(АФХ) Wp(jw)=A1(w)*ejj1(w)* ejwt= A1(w) * ej[j1(w)-wt]. Видим, что чистое запаздывание не влияет на модуль АФХ, но увеличивает сдвиг по фазе выходного сигнала. АФХ разомкнутой системы можно построить по АФХ W1(jw), где каждый радиус-вектор W1(jw) для частоты wi следует дополнительно повернуть по часовой стрелке на угол wit.

При некотором значении запаздывания t система может оказаться на границе устойчивости. (рис№2). Условие попадания на границу устойчивости имеет вид:

{A1(wкр)=1j1(wкр)- wкр* tкр= -p, wкр* tкр=p+j1(wкр), tкр= (p+j1(wкр)) /wкр, При всех значениях t<tкр замкнутая система будет устойчива,

а при t>tкр- неустойчива.

 

 

Дата добавления: 2015-07-25; просмотров: 307 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Применение критерия Найквиста при наличии астатических и консервативных звеньев.| Построение областей устойчивости методом Д-разбиения.
mybiblioteka.su - 2015-2024 год. (0.006 сек.)