
|
Читайте также: |
Логические выражения, с помощью которых представляются дискретные устройства могут содержать любые функции одного и двух аргументов (2.1) и (2.2). В этом случае для построения электрических схем необходимо выполнить техническую реализацию всех функций алгебры логики, входящих в логические выражения. Задача технической реализации всех функций алгебры логики является достаточно сложной и дорогостоящей. Избавиться от этой сложной задачи позволяют функционально-полные системы функций алгебры логики.
Система функций алгебры логики называется функционально полной, если с помощью функций, входящих в эту систему можно представить любую из 16 функций алгебры логики двух аргументов. В пятом столбце таблицы 1.6. все функции двух аргументов представлены одной их стандартных форм, которая называется совершенной дизъюнктивной нормальной формой (СДНФ). СДНФ включает в себя три функции алгебры логики
- отрицание «НЕ»,
- конъюнкцию «И»,
- дизъюнкцию «ИЛИ».
Этот состав функций «И», «ИЛИ», «НЕ» является основным функционально-полным набором функций алгебры логики.
При построении электрических схем дискретных устройств достаточно широко используются еще два функционально-полных набора, каждый из которых содержит только одну функций «И-НЕ» либо «ИЛИ-НЕ».
Таким образом, в дальнейшем будем использовать следующие три функционально-полных набора:
1. «И», «ИЛИ», «НЕ»;
2. «И-НЕ»;
3. «ИЛИ-НЕ».
Существуют и другие функционально-полные системы функций алгебры логики, но они практически не используются.
Для представления любого логического выражения любым функционально-полным набором необходимо сначала это выражение представить функционально полным набором «И», «ИЛИ», «НЕ» используя таблицу 1.6., а затем используя закон двойного отрицания и закон инверсии заданное выражение можно представить функционально-полным набором «И-НЕ» либо «ИЛИ-НЕ». Функционально-полные наборы называют базисами.
Пример 2.5. Представить логическое выражение  ~
~  базисом «И», «ИЛИ», «НЕ».
базисом «И», «ИЛИ», «НЕ».
Для этого согласно таблице 1.6. сначала избавимся от операции неравнозначности, а затем от операции равнозначности. В результате получим:
 ~
~  .
.
Согласно закону инверсии опустим знаки отрицания непосредственно на аргументы, раскроем скобки и получим следующий окончательный вариант


Для представления этого логического выражения базисом «И-НЕ» необходимо избавиться от операции ИЛИ (логического сложения). Для этого воспользуется сначала законом двойного отрицания  и получим:
и получим:
 ~
~  .
.
По закону инверсии опустим нижнюю черту двойного отрицания на аргумент
 ~
~ 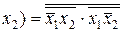 .
.
Таким образом в базисе «И-НЕ» присутствуют только две операции «И» (логическое умножение) и отрицание, которые реализуются одним логическим элементом.
Аналогично выполняется представление данного логического выражения базисом «ИЛИ-НЕ». Для этого необходимо избавиться от операции логического умножения.
 ~
~ 
Дата добавления: 2015-07-25; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема разложения в ряд функции алгебры | | | Стандартные формы функций алгебры логики |