Теорема разложения в ряд функции алгебры

Логики

Любая функция алгебры логики может быть разложена в ряд на основании теоремы разложения. Теорема разложения может быть представлена двумя формами следующим образом:

(2.15)

(2.16)

В выражениях (2.15) и (2.16) функция разложена по переменной х ₁. Тождества теоремы разложения доказываются путем подстановки в левые и правые части тождеств в начале , , а затем , . В обоих случаях тождества будут одинаковые.

Функция алгебры логики аналогично может быть разложена по любой из переменных или последовательно по всем переменным.

Пример 2.1. Разложить функцию сначала по х ₁, а затем по х ₂.

В результате разложения заданной функции получили ее стандартную форму.

Из теоремы разложения вытекают следующие соотношения, которые широко используются для упрощения функций алгебры логики:

(2.17)

(2.18)

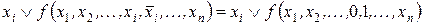(2.19)

(2.20)

Докажем справедливость выражения (2.17). Для этого функцию 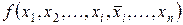левой части данного выражения разложим по переменной х_i и в результате получим

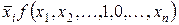(2.21)

Левую и правую части выражения (2.21) умножим на х_i согласно (2.17) и с учетом тождества и закона повторения получим:

.

Аналогично можно доказать соотношения (2.18) ¸ (2.20).

Соотношения (2.17) ¸ (2.20) позволяют сделать следующие выводы:

1. Если в логическом выражении какой-то из аргументов находится в конъюнктивной связи с одноименными аргументами или их отрицаниями, то при упрощении логического выражения вместо одноименных аргументов записывается 1, а вместо их отрицания 0.

2. Если в логическом выражении отрицание какого-либо аргумента находится в конъюнктивной связи с одноименными аргументами или их отрицаниями, то при упрощении логического выражения вместо одноименных аргументов ставится 0, а вместо их отрицаний 1.

3. Если в логическом выражении какой-то из аргументов находится в дизъюнктивной связи с одноименными аргументами или их отрицаниями, то при упрощении логических выражений вместо одноименных аргументов записывается 0, а вместо их отрицаний 1.

4. Если в логическом выражении отрицание какого-либо аргумента находится в дизъюнктивной связи с одноименными аргументами или их отрицаниями, то при упрощении логического выражения вместо одноименных аргументов записывается 1, а вместо их отрицаний 0.

Пример 2.2. Упростить логическое выражение (логическую функцию) .

Используя соотношение (2.17) получим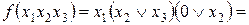

.

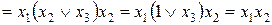Пример 2.3. Упростить логическую функцию

.

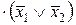Применяя соотношение (2.18) получим =

.

Пример 2.4. Упростить логическую функцию

.

Применяя соотношение (2.19) получим =

.

Дата добавления: 2015-07-25