Законы алгебры логики

Переместительный закон:

(2.1)

(2.2)

Из этого закона следует, что в выражениях алгебры логики допустима перестановка мест слагаемых и сомножителей.

Сочетательный закон:

(2.3)

(2.4)

Выражения (2.3) и (2.4) свидетельствуют о том, что при такой записи функций дизъюнкции и конъюнкции скобки можно опустить.

Распределительный закон:

(2.5)

(2.6)

Выражение (2.5) позволяет раскрывать скобки и выносить за скобки отдельные аргументы. Справедливость выражения (2.6) можно доказать с помощью таблицы истинности.

Таблица 2.1.

Наборы аргументов		Левая часть выражения (2.6)		Правая часть выражения (2.6)
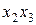
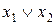
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

Из таблицы 2.1. следует, что левая часть выражения (2.6) на всех наборах аргументов равна правой части. Таким образом доказана справедливость данной записи распределительного закона.

Закон инверсии (правило Де-Моргана):

(2.7)

(2.8)

Для доказательства справедливости выражений (2.7) и (2.8) построим таблицы истинности, соответственно таблица 2.2. и таблица 2.3.

Таблица 2.2.

Наборы аргументов		Левая часть		Правая часть
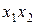
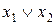
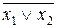
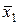
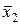
0 0
0 1
1 0
1 1

Левая и правая части выражения (2.7) равны на всех наборах аргументов.

Таблица 2.3.

Наборы аргументов		Левая часть		Правая часть
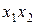
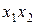
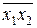
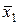
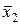
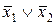
0 0
0 1
1 0
1 1

Из таблицы 2.3. следует, что выражение (2.8) справедливо.

Закон двойного отрицания:

.

Закон повторения:

(2.9)

(2.10)

Выражения (2.9) и (2.10) в доказательстве не нуждаются.

Закон поглощения:

(2.11)

(2.12)

Закон поглощения (2.11) и (2.12) докажем аналитическим путем.

.

.

Закон склеивания:

(2.13)

Доказательство аналитическое

. (2.14)

Дата добавления: 2015-07-25