Асимптотические методы. Асимптотически точная оценка. Оценки сверху и снизу.

Опр. 1: Пусть имеются ф-и f(n) и g(n). Пусть они неотриц. при дост. больших n. Говорят, что f(n)=θ(g(n)) {f(n) есть θ(g(n))}, если , для кот. можно подобрать такое значение n₀, что выполняется: 0≤с₁g(n)≤f(n)≤c₂g(n). 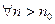. Точная асимптотическая оценка.

Опр. 2: Пусть имеются ф-и f(n) и g(n). Пусть они неотриц. при дост. больших n. Говорят, что f(n)=О(g(n)) {f(n) есть О(g(n))}, если , что 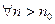выполн.: 0≤f(n)≤cg(n). Асимптотич. оценка сверху.

Говорят, что f(n)=Ω(g(n)), если , что 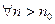выполн.: 0≤cg(n)≤f(n). Асимпт. оценка снизу

Опр. 3: Пусть имеются ф-и f(n) и g(n). Пусть они неотриц. при дост. больших n. Говорят, что f(n)=o(g(n), если 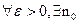, что 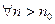0≤f(n)≤εg(n). Уточнённая асимпт. оценка сверху.

Говорят, что f(n)=ω(g(n)), если 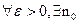, что 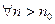0≤εg(n) ≤f(n). Уточн. асимпт. оц. снизу.

Дата добавления: 2015-07-20