
Читайте также:
|
Опр. Пусть имеется {an}. Пусть для всех членов этойпослед-ти, начиная с r-го выполняется(*): 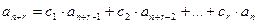 , где с1…сr=const. Тогда говорят, что на послед-ти {an} задана лин. однор. рек. соотн. с пост. коэфф. порядка r.
, где с1…сr=const. Тогда говорят, что на послед-ти {an} задана лин. однор. рек. соотн. с пост. коэфф. порядка r.
Зам.: очевидно, что зная соотношения (*) и первые r членов послед-ти можно найти любой член послед-ти. В общем случае этот способ полная лажа.
Опр.: Решить соотношение (*), значит, найти n-й член соответствующей послед-ти как ф-ю от n.
Общий метод решения:
Для того, чтобы решить соотнош. (*), достаточно найти приводящую ф-ю соответствующей послед-ти.
Пусть есть (*). Найти an=A(n). A(x)-? Рассмотрим многочлен k(x): k(x)=1-c1x-c2x-…-crxr. K(x)*A(x)=C(x). Можно показать, что мн-н С(х) обладает таким св-ом: degC(x) ≤ r-1. A(x)=C(x)/K(x).
Дата добавления: 2015-07-20; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Последовательности. Производящие функции. Операции над производящими функциями. | | | Основная теорема о рекуррентных соотношениях. |