Основная теорема о рекуррентных соотношениях.

Рассмотрим рекуррентное соотношения (**): , , 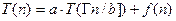где , а f(n) – некая асимптотич. ф-я.

Такие рекуррентные соотношения возникают, в частности, при математич. описании рекурсивных алгоритмов вида: имеется задача размерности n, она разбивается на а подзадач размерности n/b, которые решаются рекурсивно.

Теорма даёт правило нахождения асимптотики решения (**). В основе теоремы сравнение 2-х ф-й: f(n) и n^log_b^a. Оказывается, что та из этих ф-й, кот. растёт быстрее и задаёт асимптотику решения. В случае, если ф-и одного порядка, то любая из них задаёт асимптотику решения.

Теор. Пусть а≥1, b>1, f(n) – некая асимптотическая неотриц. ф-я. T(n) задаётся соотношением: 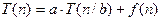, где под n/b понимается либо «пол» либо «потолок» от n/b. Тогда:

1. если f(n)=O(n^log_b^a-ε), то T(n)=θ(n^log_b^a);

2. если f(n)=θ(n^log_b^a), то T(n)=θ(n^log_b^a*log_ba);

3. если f(n)=Ω(n^log_b^a+ε), ε>0 и если выполняется условие нормирования 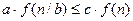, с<1 и достаточно больших n, то T(n) = θ(f(n)).

Зам.: Условие теор. не охватывает всех возможных случаев.

№5. Понятие графа, псевдографа, орграфа, мультиграфа, нагруженного графа. Изоморфизм графов. Инварианты графов. Подграфы. Теор. Эйлера о сумме степеней вершин графа.

Опр.1: Графом (простым графом) назовём совокупность 2-х множеств V и E, где V - непустое мн-во объектов произвольной природы, назыв. мн-ом вершин графа, Е – мн-во неупорядоченных пар элементов из V, назыв. мн-ом рёбер графа. G=<V, E>.

Кол-во эл-ов во мн-ве V обозначается p(G), в Е – q(G). |V|=p(G), |E|=q(G).

Опр. 2.1: Если имеется пара G=<V, E>, в кот. V (см. Опр.1), а Е (см. Опр.1), в т.ч. повторяющиеся, то такие повторяющиеся пары назыв. кратными рёбрами, а граф G=<V, E> назыв. графом с кратными рёбрами или мультиграфом.

Опр. 2.2: Пусть имеется совокупность 2-х мн-тв G=<V, E>, где V -||-, а мн-во Е – мн-во упорядоченных пар из V, тогда G назыв. ориентированным графом (орграфом), мн-во V- мн-во узлов, Е- мн-во дуг.

Опр. 2.3: -||-||-, Е- мн-во пар элементов из V, включающее в себя, в т.ч., пары одинаковых, повторяющихся элементов из V, то такие эл-ты назыв. петлями, а G- графом с петлями (псевдографом).

Опр. 2.4: Дан граф G=<V, E>. Пусть имеется некоторое мн-во М, пусть задана ф-я f: V→M и/или Е→М. Тогда говорят, что мн-во М- мн-во пометок (мн-во весов), а граф G назыв. нагруженным (взвешенным, раскрашенным, помеченным).

Опр. 3: Пусть имеется граф G, пусть в этом графе имеется ребро е0Е, е=(v_i, v_j). Будем говорить, что вершины v_i и v_j явл. концами рёбер; будем говорить, что вершины v_i и v_j инцидентны одному ребру е; будем говорить, что ребро е инцедентно вершинам v_­i и v_j. Две вершины, инцидентные одному ребру назовём смежными; два ребра, инцидентные одной вершине назовём смежными.

Опр. 4: Пусть имеется два графа G₁=<V₁, E₁> и G₂=<V₂, E₂>. Назовём данные графы изоморфными, если сущ. биекция между мн-ом их вершин, сохраняющая смежность.

Опр. 5: Если мн-во V конечное, то граф назыв. конечным.

Опр. 6: Числовые хар-ки, одинаковые для всех изоморфных графов назыв. инвариантами.

Опр. 7: Пусть дан граф G=<V, E>. Граф G`=<V`, E`> будем назыв. подграфом графа G, если V`dV и/или Е`dE. Если V`=V, то G` назыв. остовным подграфом графа G. Если остовной подграф явл. деревом, то он назыв. остовным.

Теор. (Эйлера о сумме степеней вершин графа): Сумма степеней всех вершин графа равна удвоенному кол-ву рёбер .

То же для орграфов: Сумма полустепеней захода всех узлов графа равна удвоенному числу дуг. .

---

Дата добавления: 2015-07-20