Последовательности. Производящие функции. Операции над производящими функциями.

Опр.1: Функция действительного или комплексного переменного, имеющая вид 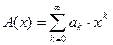назыв. производящей функцией числовой последовательности {A_n­­}.

Зам.1: понятие производящей функции позволяет свести работу с последовательностями к работе с фу-ми. Аналитич. методы работы с производящими фу-ми оказываются удобнее, чем непосредственные методы работы с последоват.

Зам.2: правая часть равенства, задающего производящую ф-ю явл. фактически разложением ф-и в ряд Тейлора в окрестности т. ноль (ряд Макларена). В силу этого последоват. может быть восстановлена по своей производящей ф-и. Для этого достаточно разложить производящую ф-ю в ряд Макларена и проанализировать общий член разложения.

Операции:

1. Линейные комбинации. Имеются послед-ти {a_n} и {b_n}. Пусть {c_n} получена из них так: 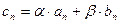, 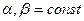. В этом случае производящая ф-я .

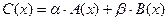2. Сдвиг начала последовательности вправо. Пусть имеется {a_n}. Пусть {b_n} получена из {a_n} так: {b_n}: b_n=0, k=0, 1, …,i-1; b_n=a_n-1, k=i, i+1,… В этом случае B(x)=x­^i­A(x).

3. сдвиг начала последовательности влево. Есть {a_n}. {b_n} получена из неё так: b_n=a_i+n, n=0, 1,… B(x) = .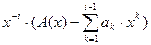

4. Частичные суммы. Есть {a_n}. {b_n} получена из неё так: 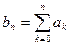. B(x)=A(x)/(1-x)/

5. Дополнительные частичные суммы. Есть {a_n}. {b_n} получена из неё так: . B(x)= .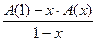

6. Есть {a_n}. {b_n} получена из неё так: b_n=n*a_n. B(x)=x*A`(x).

7. Есть {a_n}. {b_n} получена из неё так: b_n=a_n/(n+1). B(x)= .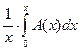

Дата добавления: 2015-07-20