Асимптоты графика функции.

Асимптотой графика функции у = f (x) называется прямая, обладающая тем свойством, что расстояние от точки М (х, f (x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Возможны два способа удаления точки М (х, f (x)) графика функции у = f (x) от начала координат в бесконечность: 1) аргумент х стремится к некоторой точке х₀, а соответствующее значение функции у = f (x) стремится к бесконечности; 2) аргумент х стремится к бесконечности. Поэтому существуют два типа асимптот: вертикальные и наклонные.

Прямая х = х₀ называется вертикальной асимптотой графика функции у = f (x), если хотя

бы один из односторонних пределов f (x₀ -0) = (предел слева) или f (x₀ + 0) = = (предел справа) равен +¥ или -¥ (см. рис. 19.16).

Как видно из рисунка 19.16, расстояние между точкой
М (х, f (x)) графика функции у = f (x) и вертикальной прямой х = х₀ равно d = ç х - х₀ ç. При х ® х₀ точка М (х, f (x)) удаляется в бесконечность, а d = ç х - х₀ ç® 0 при х ® х₀, т. е. это и означает, что х = х₀ – уравнение вертикальной асимптоты.

Пример 19.2. Рассмотрим функции у = , х Î (-¥,0) (0,+¥) и у = log₂ x, x Î (0,+¥), для которых прямая х = 0 является вертикальной асимптотой.

1) у = , х Î (-¥,0) (0,+¥).

f (+0) = = ,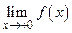

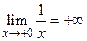f (- 0) = = .

Это и означает, что прямая х = 0 является вертикальной асимптотой функции у = , а точка х₀ = 0 – точка разрыва второго рода.

2) у = log₂ x, x Î (0,+¥).

f (+0) = 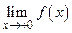= , поэтому прямая х = 0 является вертикальной асимптотой функции у = log₂ x, хотя точка х₀ = 0 формально и не является точкой разрыва функции у = log₂ x.

Заметим, что вертикальные асимптоты графика функции возникают в точках разрыва второго рода или на границе области определения функции.

Прямая У = kx + b называется наклонной асимптотой графика функции у = f (x) при
х ® +¥ (х ® - ¥), если функцию у = f (x) можно представить в виде

f (x) = kx + b +a(х), (19.1)

где a(х) ®0 при х ® +¥ (х ® - ¥).

При х ® +¥ наклонная асимптота называется правой, а при х ® - ¥ – левой. При k = 0 асимптота называется горизонтальной.

Выясним геометрический смысл наклонной асимптоты, рассмотрев для определенности случай, когда х ® +¥.

М (х,у) – точка графика функции у = f (x), У = kx + b – наклонная асимптота графика функции при х ® +¥, N (х,у) – соответствующая точка асимптоты (см. рис. 19.17). Тогда ú MN ÷ = ÷ y - Y ÷ = ÷ f (x) - kx - b ÷ =
= ú a (x)÷ ®0 при х ® +¥. Из прямоугольного треугольника MNР ясно, что 0 < d < ú a (x)÷, поэтому d ®0 при х ® +¥, т. е. график функции неограниченно приближается к асимптоте при х ® +¥.

Теорема 19.8. Для того, чтобы график функции у = f (x) имел при х ® +¥ (х ® - ¥) наклонную асимптоту у = kx + b, необходимо и достаточно, чтобы существовали пределы

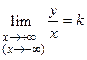и .

Доказательство. Для определенности рассмотрим случай правой наклонной асимптоты, т. е. х ® +¥.

Необходимость. Пусть У = kx + b – наклонная асимптота графика функции у = f (x) при
х ® +¥, тогда

у = f (x) = kx + b +a(х), где a (x) ®0 при х ® +¥.

Из этого представления вытекает, что существует предел

, т. к. и – б. м. при х ® +¥, и существует предел .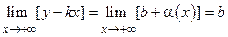

Достаточность. Пусть существуют оба предела и .

Из второго предела вытекает, что по теореме 16.4 справедливо равенство

у - kx = b +a(х), где a (x) ®0 при х ® +¥,

т. е. у = f (x) = kx + b +a(х). Но это и означает, что прямая У = kx + b является асимптотой графика функции у = f (x).

Пример 19.3. Рассмотрим функцию у = .

Так как у = f (x) = х + 2 + , где a (x) = ® 0 при х ® ±¥, то прямая У = x + 2 является левой и правой наклонной асимптотой графика функции.

Замечание. Для рациональной функции (отношения двух многочленов) левая и правая асимптоты совпадают.

План полного исследования функции и построения ее графика.

При полном исследовании функции и построения ее графика рекомендуется использовать следующую схему:

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность (является ли график функции симметричным относительно оси Оу, или начала координат, или общего вида).

3. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.

4. Исследовать функцию на непрерывность, найти точки разрывы функции, асимптоты.

5. Найти интервалы монотонности функции и ее экстремумы.

6. Найти интервалы выпуклости и вогнутости и точки перегиба и графика функции.

7. Построение графика функции.

Заметим, что исследовании функции проводится одновременно с построением графика.

Пример 19.4. Провести полное исследование и построить график функции

.

Решение. Исследование и построение проведем по намеченной выше схеме, нанося каждый шаг исследования на график.

1. D(y) = (-¥; -2) (-2;2) (2;+¥), т. к. рациональная функция определена всюду, кроме нулей знаменателя х = ±2.

2. Четность-нечетность. Т. к.

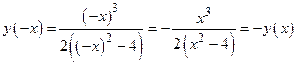, то функция у = f (x) нечетная и ее график симметричен относительно начала координат О(0,0).

3. Найдем точки пересечения графика функции с осями координат и интервалы знакопостоянства:

с Оу: у(0) = 0; сОх: у =0 при х = 0.

Итак, график функции пересекает оси координат только в точке О(0,0).

у:

Интервалы знакопостоянства функции:

Наносим полученные факты на график (см. рис. 19.18), где отмечена точка графика О(0,0), а штриховка указывает, выше или ниже оси Ох лежат точки графика на данном участке.

4. Непрерывность, точки разрыва, асимптоты.

Функция у = f (x), являясь рациональной дробью, непрерывна (и дифференцируема) всюду, где определенна как элементарная. Точки х = ±2 являются точками разрыва функции. Определим их характер. В силу нечетности функции, достаточно рассмотреть одну из этих точек, например х₀ = 2. Найдем односторонние пределы функции в этой точке:

f (2-0)

= , f (2+0) = ,

т.е. х₀ = 2 – точка разрыва второго рода, а прямая х = 2 является вертикальной асимптотой. В силу симметричности, х = -2 тоже точка разрыва второго рода, а прямая х = -2 является вертикальной асимптотой. Наносим эти факты на график.

Найдем наклонную асимптоту У = kx + b графика функции у = f (x) при х ® ¥, т. е. исследуем поведение функции на бесконечности. Так как существуют пределы

,

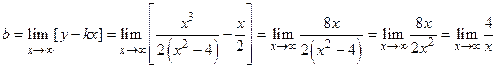= 0,

то прямая У = является наклонной асимптотой, причем левой и правой.

5. Монотонность, экстремумы.

Найдем интервалы убывания и возрастания, точки максимума и минимума, исследовав первую производную функции:

у¢ =

=

Найдем точки возможного экстремума функции из условия у¢ = 0, т. е. х = ±2 – стационарные точки. Тогда

y ¢:

х ₁= -2 – точка максимума и у _max= f (-2 ) = - ,

х ₂= 2 – точка минимума и у _min= f (2 ) = .

Интервалы возрастания: (-¥;-2 ) (2 ;+¥),

интервалы убывания: (-2 ; -2) (-2;2) (2;2 ).

Наносим точки экстремума на график.

6. Выпуклость, вогнутость, точки перегиба.

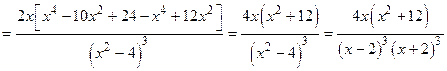
Тогда у¢¢= 0 при х =0 и

у¢¢:

Точка х ₀ = 0 – точка перегиба, у (0)=0, у¢ (0)=0, т.е. у = 0 – уравнение касательной в точке перегиба. Хотя в точках ±2 вторая производная меняет знак, они не являются точками перегиба, т.к. в этих точках функция не определена. Учитывая пункты 5 и 6, заканчиваем построение графика функции.

Дата добавления: 2015-07-20