Читайте также:
|
1. Вычисление числа е.
Запишем формулу Маклорена функции у = ех с остаточным членом в форме Лагранжа
ех = 1+ 
.
Положив х =1, получим
ех = 1+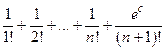 
» 1+ 
,
где с Î (0;1), а погрешность | Rn (x)| = | 
|•| Rn (x)| ≤ 
< e.
Если требуется вычислить значение с с точностью e = 0,001, то число п определяется из неравенства < 0,001, или (п +1)! > 3000, т. е. п = 6.
Таким образом,
ех = 1+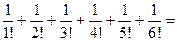 
2,718.
2. Происхождение эквивалентности б. м.
Первый замечательный предел: sin x ~ x получается из формулы (18.50) отбрасыванием б. м. более высокого порядка, чем х ®0:
sin x 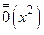= x + 
~ x.
Далее, из формулы (18.51) получаем
1- cos x = 
~ 
.
Аналогично получаем
ех – 1 = x + 
~ x,
ln (1+ х) = x + ~ x,
(1+ x) α- 1 =ax + ~ a x.
Приложения формулы Тейлора (Маклорена) покажем на примерах позже.
Дата добавления: 2015-07-20; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула Маклорена некоторых элементарных функций. | | | Применение производных к исследованию функций и построению графиков. |