Логарифмическая производная

Вычислим производную функции y = ln| x |, x ≠ 0, (см. рис. 18.2).

При x >0 y =ln x и (ln x)¢= ,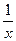

При x <0 y =ln (- x) и (ln(- x))¢= 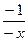= 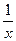поэтому

(ln| x |)¢= 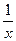. (18.13)

Пусть функция y=f (x) дифференцируема и отлична от нуля. Вычислим производную функции ln| x | = ln| f (x)|.

По правилу дифференцирования сложной функции, учитывая формулу (18.13), получим

(ln| x |)¢= или (ln| у |)¢= . (18.14)

Это и есть логарифмическая производная функции f (x), т.е. производная от логарифма модуля функции.

В качестве примера найдем с помощью логарифмической производной производную показательно-степенной функции

y=u (x) ^{v ( x )},

где u = u (x)>0 и v = v (x) некоторые дифференцируемые функции. Так как ln y = v (x)ln u (x), то по формуле (18.14)

=[ v (x) ln u (x)]¢= v¢ (x) ln u (x)+ v (x) ,

отсюда окончательно получаем

y¢ = u (x) ^{v ( x )}[ v¢ (x) ln u (x) + v (x) ],

или в краткой записи

y¢ = u^v ln u • v¢+ v u^{v -1} u¢.

производная производная

показательной степенной

функции функции

Пример 18.11. y=x^α, α Î R. Найдем у¢, для чего найдем логарифмическую производную функции у=х^α:

ln y=α ln х, (ln y)¢= = 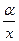, у¢=х^α 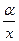= α х^{α- 1}.

Итак:

(х^α)¢= α х^{α- 1}.

Пример 18.12. Найдем у ¢, если у= .

Решение. Вновь воспользуемся логарифмической производной:

ln| y | = ln 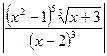=5 ln | x ²-1| + 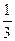ln| x +3|-3ln | x -2|,

= 5• ,

окончательно получим

у¢ = .

Дата добавления: 2015-07-20