Читайте также:
|
Показательная функция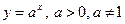 
является монотонной функцией на ее области определения. Это гарантирует существование обратной ей функции. Эта обратная функция обозначается так: 
.
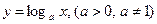Свойства логарифмической функции.
1. 
.
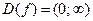2. E (f)= R.
3. четность и нечетность не рассматривается, так как область определения не симметрическое множество.
4. Если a > 1, то функция возрастает на D.
Если 0 < a < 1, то функция убывает на D.
5. Множество точек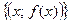 
на плоскости логарифмическая кривая. Получается из графика функции 
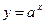с помощью преобразования симметрии относительно прямой 
.
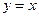Дата добавления: 2015-07-25; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обратная функция | | | Логарифмические уравнения |