Свойства логарифмов

1. Основное логарифмическое тождество. Если x > 0, то , .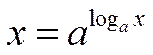

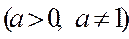2. Логарифм основания равен единице. , 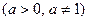. Так как .

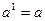3. Логарифм единицы равен нулю. 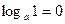, 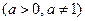. Так как .

4. Логарифм произведения равен сумме логарифмов сомножителей.

а) 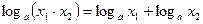, если , .

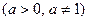в) 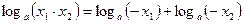, если , .

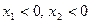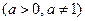Эти две формулы можно объединить в одну:

с) 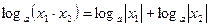, если , .

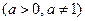Доказательство пункта 4а). Обозначим 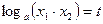, , 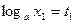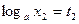. Тогда по определению логарифма имеем: 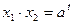, , 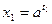, , 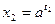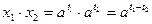т.е. 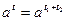. Отсюда 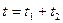, т.е. 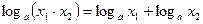. ч.т.д.

Аналогично доказывается пункт 4в).

Замечание. При использовании формул 4а) и 4в) мы сужаем область определения: левая часть определена при , а правая при или 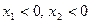. При использовании этих формул возможна потеря решения. При использовании формулы 4с) мы расширяем область определения: левая часть определена при , а правая при . При использовании этой формулы можно приобрести постороннее решение. Что хуже?

5. Логарифм частного равен разности логарифмов делимого и делителя.

а) 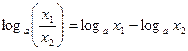, если , .

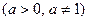в) , если , .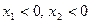

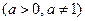Объединив эти две формулы, получим:

с) 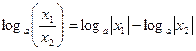, если , .

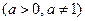Доказательство аналогично пункту 4 (самостоятельно).

6. Логарифм степени равен произведению показателя степени на логарифм основания степени.

а) , если , .

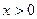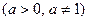в) 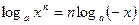, если n четное и , .

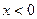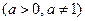В общем случае, с учетом замечания к пункту 4, можно записать:

с) 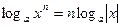, если , .

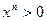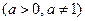7. Логарифм корня: , , .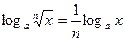

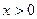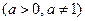8. Логарифм рациональной степен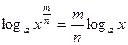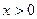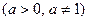и: , , . Или , если , .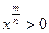

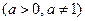9. Формула возведения в степень основания логарифма и выражения под знаком логарифма: 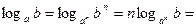, , 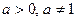b > 0.

10. Формула перехода к новому основанию: 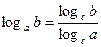, b > 0, , .

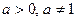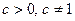Доказательство пункта 10. .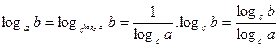

11. Если c = b, то , , .

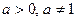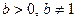12. , , 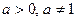x > 0, y > 0.

Доказательство.

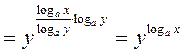. Ч.т.д.

13. Знаки логарифмов.

Если число и основание лежат по одну сторону от единицы, то логарифм положителен. Если по разные стороны, - то отрицателен:

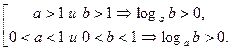
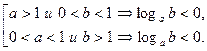
Примеры.

1. Представить степень с основанием a в виде степени с основанием b.

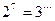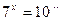а) ; b) ; c) .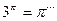

2. Вычислить.

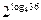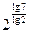a) ; b) ; c) ; d) ; e) .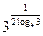

Дата добавления: 2015-07-25