Читайте также:
|
Показательная функция - это функция вида
Свойства:
1. 
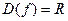
2. 
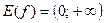
3. Не является четной и не является нечетной
4. 
- горизонтальная асимптота
5. При 
6. 
- показательная кривая
Это пример графика функции (например, 
).
Это пример графика функции (например, 
).
Для показательных выражений имеем сравнения:
1) 
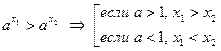
2) 
3) 
Функция 
при 
и 
называется показательной.
Почему не берется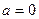 
и 
При 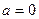имеем при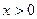 
- это постоянная функция.
При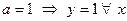 
тоже постоянная функция.
Выражение 
при 
имеет смысл только в случае, когда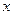 
- рациональное число, т.е. число вида 
и 
- нечетное, т.е. для отдельных точек. Степень с отрицательным основанием и иррациональным показателем или с четным знаменателем показателя не определена. Не определено также выражение 
или 0 в отрицательной степени.
Дата добавления: 2015-07-25; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проект рациональных технологий производства сельскохозяйственной продукции | | | Показательные уравнение и неравенства |