Дифференциальные уравнения.

Определение: Дифференциальным уравнением (д.у.) называется уравнение связывающее функцию, ее производные и аргумент: .

Определение: порядком д.у. называется порядок старшей производной уравнения.

Примеры: а) - уравнение третьего порядка;

б) 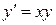- уравнение первого порядка.

Рассмотрим основные виды д.у. первого порядка: .

I Уравнения с разделяющимися переменными: .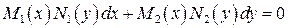

Для решения данного уравнения разделим обе части на , проинтегрировав обе части найдем общее решение: .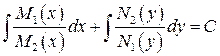

Пример 1. Найти общее решение уравнения: .

Решение: Разделим обе части на

, проинтегрируем

.

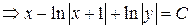Ответ: .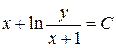

Пример 2. Найти частное решение: , .

Решение: Чтобы найти частное решение, находим вначале общее решение, опираясь на начальные условия найдем константу С и подставив ее в общее решение, получаем частное решение.

;

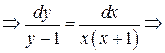
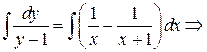
Общее решение: при , имеем: .

Ответ: - частное решение.

II Однородные уравнения.

Однородное уравнение решатся заменой .

Пример 3. Найти общее решение .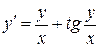

Решение: Вводим замену и получаем: .

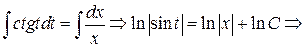
Ответ: .

Пример 4. Найти частное решение .

Решение: Заменяем .

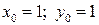, при имеем: .

Ответ: .

III Линейные уравнения.

.

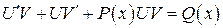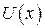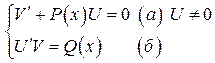Решение: Пусть ; чтобы найти и составим систему: , из строки 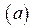находим , подставив в получаем: 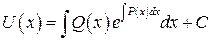, с учетом имеем: 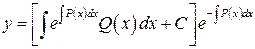- решение линейного уравнения.

IV Уравнение Бернулли.

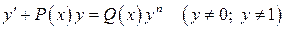
Уравнение Бернулли решается аналогично линейному уравнению, т.е. .

Пример 5. Найти общее решение уравнения

(линейное д.у.)

Решение: 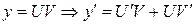, подставим и в уравнение : .

Составим систему: , т.к. , то из имеем: 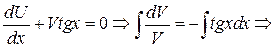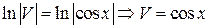, подставим 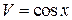в : .

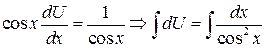
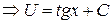Ответ: 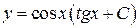или .

Пример 6. Решить задачу Коши 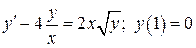. Данное уравнение – Бернулли

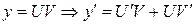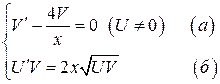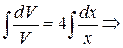
Решение: , подставив и в уравнение имеем: , из : , подставим в : .

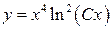- общее решение, с учетом н.у. имеем: .

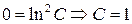Ответ: .

Линейные однородные уравнения с постоянными коэффициентами.

Пусть - линейное однородное д.у.

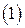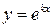
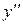Решение: ищем в виде и подставив , и в 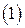получаем характеристическое уравнение: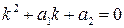

При решении уравнения возможны следующие варианты:

: Дискриминант , тогда корни уравнения 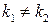и решение

уравнения имеет вид: .

: .

: .

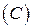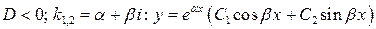Пример 7. Найти общее решение уравнения .

Решение: Запишем характеристическое уравнение: , его корн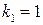и и 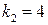(случай А).

Ответ: .

Пример 8: Найти общее решение .

Решение: 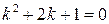его корни 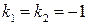(случай В).

Ответ: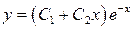

Пример 9. Найти общее решение уравнения .

Решение: . .

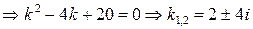Ответ: .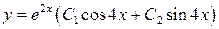

Линейные неоднородные дифференциальные уравнения.

- линейное неоднородное д.у., где

I 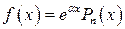, где - многочлен n – й степени.

Решение линейного неоднородного д.у. – есть сумма двух решений:

где - общее решение линейного неоднородного д.у., соответствующего данному уравнению ,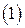

если 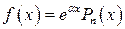, то , где - многочлен n – й степени с неопределенными коэффициентами; 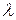- кратность корня по отношению и .

Пример 10. Решить уравнение .

Решение: . ;

Частное решение имеем в виде: . 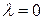, т.к. 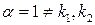. Чтобы найт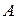и и 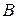необходимо найти , 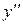и подставить в :

-5

.

Составим систему уравнений, чтобы найти А и В. Приравняв коэффициенты при и имеем:

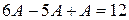
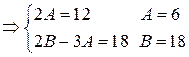
Ответ: .

Пример 11. Решить уравнение .

Решение: Решение ищем в виде: 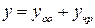. Линейное однородное д.у.:

.

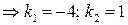
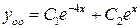Частное решение ищем виде: 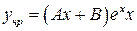, т.к. то .

-4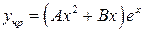

= .

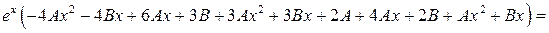
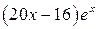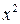
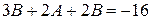
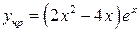
Ответ: .

II ; в этом случае , где , и -

s – степени с неопределенными коэффициентами.

Пример 12. Решить уравнение: .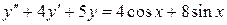

Решение: .

, .

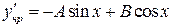
Соберем коэффициенты при и :

	5A+4B-A=4
	5B-4A-B=8

Дата добавления: 2015-07-20