
|
Читайте также: |
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 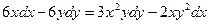
10. 
Задача 4. Однородные дифференциальные уравнения. Найти общее решение.
1. 
2. 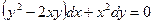
3. 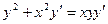
4. 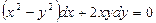
5. 
6. 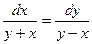
7. 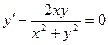
8. 
9. 
10. 
Задача 5. Линейные дифференциальные уравнения первого порядка
1. 
2. 
3. 
4. 
5. 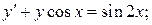
6. 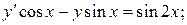
7. 
8. 
9. 
10. 
Задача 6. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
1. 
2. 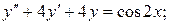
3. 
4. 
5. 
6. 
7. 
8. 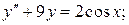
9. 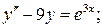
10. 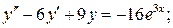
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ
Дата добавления: 2015-07-25; просмотров: 99 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Частные решения ЛНДУ специального типа. Метод вариации произвольных постоянных. | | | РАБОТЫ №3 |