Читайте также:
|
Обыкновенное дифференциальное уравнение называется однородным если при замене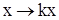 
, а 
оно не меняется.
Другими словами, если уравнение можно привести к виду
(4)
где f – любая функция, то оно является однородным.
Однородное уравнение приводится к уравнению с разделяющимися переменными типа (3) с помощью подстановки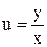 
.
Пример: решить уравнение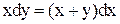 
.
Покажем, что это уравнение однородное. Для этого поделим его обе части на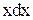 
.
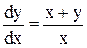
Поделив почленно правую часть на x:
.
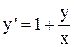Слева стоит производная y, а справа функция, зависящая только от 
. Уравнение является однородным. Применим замену 
.
Сократим на u и поделим на x:
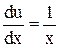
Возвращаясь к исходной неизвестной функции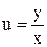
.
Кроме этого, есть еще решение 
, которое было потеряно при делении на x.
Дата добавления: 2015-07-25; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОДУ первого порядка с разделяющимися переменными. | | | Линейные ДУ первого порядка. |