
|
Читайте также: |
1) Если дифференциальное уравнение имеет вид:
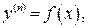 (9)
(9)
т. е. правая часть не содержит у, у ¢ и т.д. до n-1 производной функции y, то ДУ решается n-кратным последовательным интегрированием:
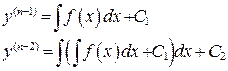
и т.д. пока не будет найдена искомая функция y(x).
Пример: решить ДУ 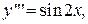
Интегрируем это выражение в первый раз

И далее
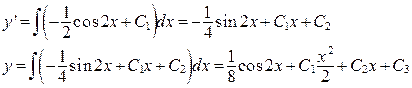
Итак: 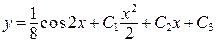
2) Если дифференциальное уравнение имеет вид:
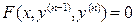 (10)
(10)
т.е. в уравнении отсутствуют все младшие производные и сама функция, кроме двух последних производных 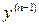 и
и 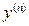 . Тогда, введя новую функцию
. Тогда, введя новую функцию 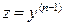 и, соответственно
и, соответственно 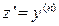 получим ОДУ первого порядка вида
получим ОДУ первого порядка вида  . Это уравнение можно решать одним из вышеописанных способов для уравнений первого порядка.
. Это уравнение можно решать одним из вышеописанных способов для уравнений первого порядка.
Пример.
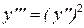
Решение
Данное дифференциальное уравнение второго порядка не содержит явно искомую функцию 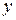 и ее первую производную y’. Введем новую функцию
и ее первую производную y’. Введем новую функцию 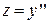 , тогда
, тогда 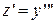 . Получим уравнение:
. Получим уравнение:
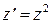
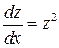
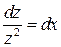
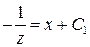

Вернемся к первоначальной переменной:
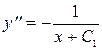
Последовательно интегрируя, получим:
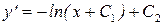
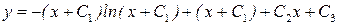

Для простоты можно переобозначить 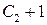 на
на 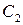 , а
, а 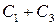 на
на  , тогда общее решение примет вид:
, тогда общее решение примет вид:
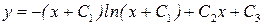
3) Если дифференциальное уравнение второго порядка имеет вид:
 , (11)
, (11)
т.е. если в уравнении отсутствует явно переменная x.
Тогда проведем замену 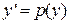 , считая производную функцией от y. Тогда по формуле дифференцирования сложной функции:
, считая производную функцией от y. Тогда по формуле дифференцирования сложной функции: 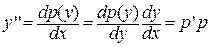 . И, подставив все эти выражения в исходное ДУ, получим его в виде дифференциального уравнения первого порядка относительно функции p и переменной y:
. И, подставив все эти выражения в исходное ДУ, получим его в виде дифференциального уравнения первого порядка относительно функции p и переменной y: 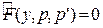 . Его можно решать методами, описанными выше.
. Его можно решать методами, описанными выше.
Пример: решить ДУ 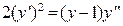
Видно, что в этом уравнении второго порядка отсутствует в явном виде переменная x. Тогда, применяя описанную выше замену 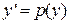 и
и 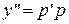 , получим:
, получим:


или 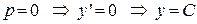 - первое решение ДУ.
- первое решение ДУ.
Продолжая решать первое уравнение
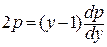
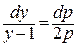
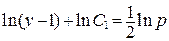
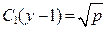

Возвращаемся к исходной функции y(x):
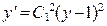
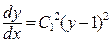
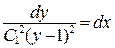
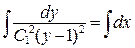
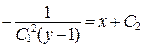

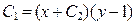 , где переобозначили
, где переобозначили 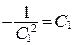
Итак, первое решение ДУ 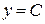 , второе
, второе 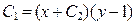 .
.
Дата добавления: 2015-07-25; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнения Бернулли. | | | Однородные (ЛОДУ). |