Читайте также:
|
а) 
Составим характеристическое уравнение:
Решим его, используя формулу корней квадратного уравнения:
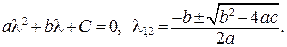
Получим корни:
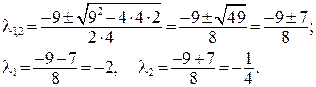
Поскольку 
и 
то общее решение запишем в виде (14):
б)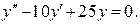 
Характеристическое уравнение:
его корни найдем по формуле корней квадратного уравнения:
Поскольку 
то общее решение запишем в виде (15):
в) 
Характеристическое уравнение:
его корни найдем по формуле корней квадратного уравнения:
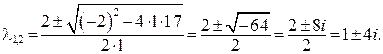
Получим комплексно сопряженные корни 
где а =1, b =4.
Решение запишем в виде (16):
г)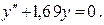 
Характеристическое уравнение:
Решим его:
— комплексно сопряженные корни вида где а = 0, b = 1,3. Решение запишем в виде (16), при этом учтем, что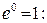 
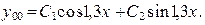
Дата добавления: 2015-07-25; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однородные (ЛОДУ). | | | Линейные неоднородные дифференциальные уравнения (ЛНДУ). |