Читайте также:
|
Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
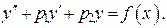(18)
Здесь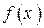 
— известная функция, непрерывная на некотором промежутке.
Согласно теореме о структуре общего решения линейного неоднородного ДУ общее решение ДУ (18)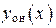 
есть сумма общего решения 
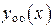соответствующего однородного уравнения (15) и любого частного решения 
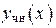неоднородного уравнения (18), т. е.
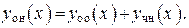(19)
Рассмотрим, в каком виде можно искать частное решение 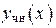ДУ (18), когда правая часть уравнения 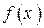имеет специальный вид.
Пусть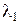 
и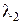 
корни характеристического уравнения (13), а правая часть уравнения имеет вид:
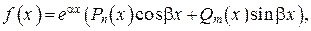(20)
где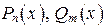 
— многочлены от х степеней n и m соответственно с известными коэффициентами.
Тогда частное решение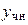 
следует искать в виде:
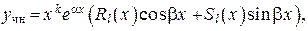(21)
где k — кратность корня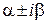 
характеристического уравнения:
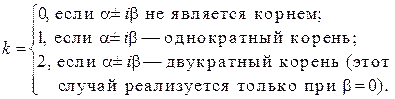
При этом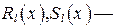 
многочлены от х степени 
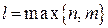с
некоторыми, пока неизвестными, коэффициентами. Неизвестные коэффициенты многочленов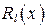 
и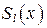 
находят методом неопределенных коэффициентов.
Пример 2.3. Найти общее решение линейных неоднородных ДУ 2-го порядка с постоянными коэффициентами:
а)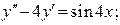 
б)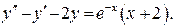 
Дата добавления: 2015-07-25; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Решение. |