Читайте также:
|
а) 
Найдем общее решение соответствующего однородного ДУ:
Характеристическое уравнение:
Поскольку 
и 
то общее решение запишем в виде (17), при этом учтем, что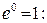 
Найдем частное решение неоднородного уравнения. Правая часть уравнения 
Сравнивая ее с видом (20) 
заключаем, что 
Определим параметры частного решения (21). Учитывая, что 
а 
получим, что 
не является корнем характеристического уравнения, поскольку корни 
Следовательно, k = 0. Найдем 
Следовательно, порядок многочленов R и S равен 0, т. е. R 0 = A, а S 0 = B, где А и В — некоторые неизвестные пока коэффициенты. Подставив полученные параметры в 
имеем:
Коэффициенты А и В определим из условия, что функция у чн — решение уравнения и поэтому должна ему удовлетворять. Найдем 
и 
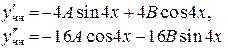
и подставим в исходное уравнение:
Приравняем коэффициенты при 
и 
в правой и левой частях полученного равенства:
Итак,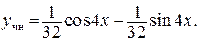 
Тогда согласно (19) общее решение неоднородного ДУ имеет вид:
б)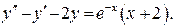 
Найдем общее решение соответствующего однородного ДУ:
Характеристическое уравнение:
Найдем его корни по формуле (17):
Поскольку и то общее решение запишем в виде (17):
Найдем частное решение неоднородного уравнения. Правая часть уравнения 
Сравнивая ее с видом (20) заключаем 
Определим параметры частного решения (21). Учитывая, что 
а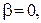 
получим, что 
однократный корень характеристического уравнения, поскольку корни 
Следовательно, k = 1. Найдем 
Следовательно, порядок многочленов R и S равен 1, т. е.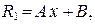 
а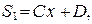 
где А, В, С, D — неизвестные коэффициенты. Подставляя полученные параметры в имеем:
Для определения коэффициентов А и В найдем и
и подставим в исходное уравнение:
Разделим обе части уравнения на 
и приведем подобные члены:
Приравняем коэффициенты при одинаковых степенях х в правой и левой частях уравнения:
Итак, 
Тогда согласно (19) общее решение неоднородного ДУ имеет вид:
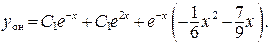
Литература.
1. Н.С. Пискунов, Дифференциальное и интегральное исчисление. Том 1,2. 1972-2000.
2. А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа для втузов. Москва: “Наука”. Главная редакция физико-математической литературы, 1973.
3. Г.М. Берман, Сборник задач по курсу математического анализа (для втузов). Москва: “Наука”. 1985.
4. П. Е. Данко, и др. Высшая математика в упражнениях и задачах: Учебное пособие для втузов. В 2-х ч. 1980 – ч.1, 1984 – ч.2.
Дата добавления: 2015-07-25; просмотров: 107 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные неоднородные дифференциальные уравнения (ЛНДУ). | | | Степенные ряды. |