
Читайте также:
|
Линейные однородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
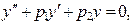 (12)
(12)
где р 1 и р 2 — действительные числа.
Согласно теореме о структуре общего решения линейного однородного ДУ достаточно найти два линейно независимых частных решения 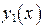 и
и 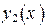 уравнения (12), чтобы записать общее решение:
уравнения (12), чтобы записать общее решение:
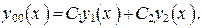
Где y00 – общее решение однородного уравнения.
Будем искать решение уравнения (12) в виде 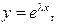 где
где 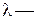 некоторая постоянная. Чтобы определить
некоторая постоянная. Чтобы определить 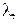 подставим
подставим 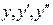 в уравнение (12).
в уравнение (12).
В результате подстановки получим уравнение 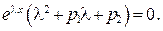
Так как 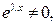 то
то
 (13)
(13)
Квадратное уравнение (13) называют характеристическим уравнением для ДУ (15), а его корни 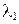 и
и 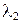 характеристическими числами. При решении характеристического уравнения (16) могут возникнуть три случая:
характеристическими числами. При решении характеристического уравнения (16) могут возникнуть три случая:
а) Корни 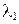 и
и 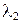 действительные и различные. Тогда общее решение уравнения (15) будет иметь вид:
действительные и различные. Тогда общее решение уравнения (15) будет иметь вид:
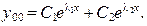 (14)
(14)
б) Корни 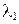 и
и 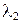 действительные и равные,
действительные и равные, 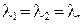 Общее решение уравнения (15) будет иметь вид:
Общее решение уравнения (15) будет иметь вид:
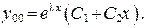 (15)
(15)
в) Корни 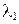 и
и 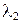 комплексно сопряженные,
комплексно сопряженные, 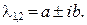 Тогда общее решение уравнения (12) примет вид:
Тогда общее решение уравнения (12) примет вид:
 (16)
(16)
Пример 2.2. Найти общие решения линейных однородных ДУ 2-го порядка с постоянными коэффициентами:
а)  б)
б) 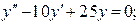
в) 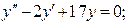 г)
г) 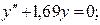
Дата добавления: 2015-07-25; просмотров: 34 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ДУ, допускающие понижение порядка. | | | Решение. |