Читайте также:
|
1.1. Линейным однородным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида:
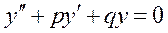, (32)
где коэффициенты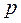 
и 
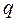- некоторые действительные числа.
1.2. Есл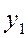и 
и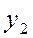 
- линейно независимые решения уравнения (32), то функция 
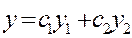, где 
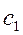и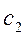 
- произвольные постоянные, является общим решением уравнения.
1.3. Для нахождения частных решений уравнения (32) составляют характеристическое уравнение:
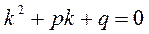(33)
которое получается из уравнения (32) заменой в нем производных искомой функции соответствующими степенями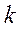 
, причем сама функция заменяется единой.
1.4. Уравнение (33) является уравнением 2-ой степени и имеет два корня
(действительных или комплексных, среди которых могут быть и равные).
Тогда общее решение дифференциального уравнения (32) стремится в зависимости от характера корней уравнения (33):
1) каждому действительному простому корню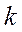 
в общем решении соответствует слагаемое вида 
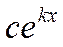; тогда общее решение уравнения (11) записывается следующим образом: 
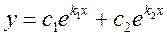, где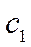 
, 
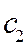- произвольные постоянные, 
, 
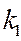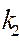- корни характеристического уравнения;
2) действительному корню кратности 2 в общем решении соответствует слагаемое вида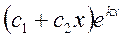 
, т.е. 
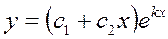, где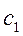 
и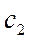 
- постоянные, 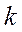- корень характеристического уравнения;
3) паре комплексных сопряженных корне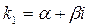й 
и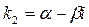 
в общем решении соответствует слагаемое вида
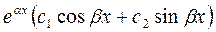, т.е.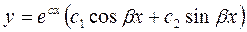 
Дата добавления: 2015-07-25; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные дифференциальные уравнения первого порядка. | | | Линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами. |