Интегрирование по частям.

Этот метод, также как и метод подстановки, который мы только что рассмотрели, принадлежит к числу основных методов интегрирования.

Пусть 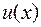и 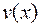– две дифференцируемые функции от 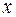. Тогда

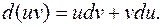
Интегрируя обе части этого равенства, получаем:

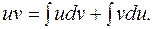
Отсюда:
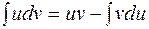(20)

Последняя формула называется формулой интегрирования по частям.

Из формулы (20) следует, что интеграл 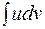приводится к интегралу 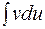, который в результате её применения оказывается более простым, чем данный, или даже табличным.

Для применения формулы интегрирования по частям к некоторому интегралу 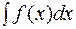следует подынтегральное выражение 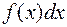представить в виде произведения двух множителей: u, dv. При этом надо прежде всего установить, какая функция принимается равной u и что относится к dv. Затем по установленному выражению u надо дифференцированием найти du, а по известному dv определить интегрирование v. Таким образом, для применения формулы (20) потребуется выполнить одно дифференцирование для определения du и одно интегрирование для определения v. Для выбора u и dv нельзя дать никаких общих указаний, за исключением того, что

а) dx должно быть частью множителей dv;

б) функцию v(x) можно найти интегрированием;

в) в качестве u(x), берется функция, которая при дифференцировании упрощается.

Укажем несколько типов интегралов, вычислять которые удобно интегрированием по частям;

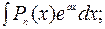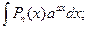1) 2) 3)

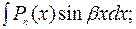
4)

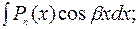
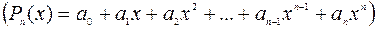
В этих интегралах за u принимается 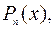что приведет к интегралу сходного типа, но уменьшит показатель степени x на единицу. После n - кратного применения этого приема получим один из табличных интегралов:

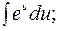
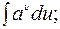
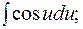
5) 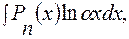за u принимаем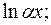

6) 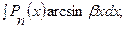за u принимаем ;

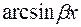7) 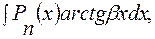за u принимаем ;

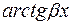Дата добавления: 2015-07-25