Основные теоретические знания

1.Площадь фигуры, ограниченной графиком непрерывной функции y=ƒ(x) (ƒ(x)≥0), прямыми x=a и x=b отрезком (a,b) оси OX или площадь криволинейной трапецией ограниченной дугой графика функции y=ƒ(x), a≤x≤b (рис.2), вычисляется по формуле

(25)

Рис. 5

2.Площадь фигуры ограниченной графиками непрерывных функций и , и двумя прямыми

x=a, x=b (рис.3) определяется по формуле

X=a

X=b

y  

Рис. 3

Рис.6

x

(26)
Задача №1.

Вычислить площадь фигуры ограниченной параболой и прямой y=x+1.

Найдем абциссы точек пересечения прямой y = x+1 с

параболой

Решая систему уравнений

Получаем . Это и есть пределы интегрирования.

Вершину параболы наёдем по формуле;

,

,

.

Найдем ординаты точек пересечения.

,

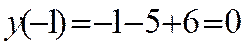Имеем (-1;0) и (-7;8)

Построим фигуру.

Искомая площадь фигуры согласно по формуле (25) такова:

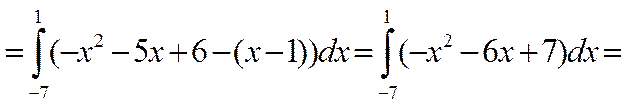
Ответ:Площадь искоймой фигуры равна.

Задача №2.

Вычислить площадь фигуры ограниченной параболой

+5x-6 и прямой y=x+1.

Найдем абциссы точек пересечения прямой

y=x+1 с параболой +5x-6

Решая систему уравнений

Для построения фигуры найдем координаты вершины параболы по формуле

Найдем ординаты точек пересечения.

Имеем (-1;0) и (-7;-8)

Построим фигуру.

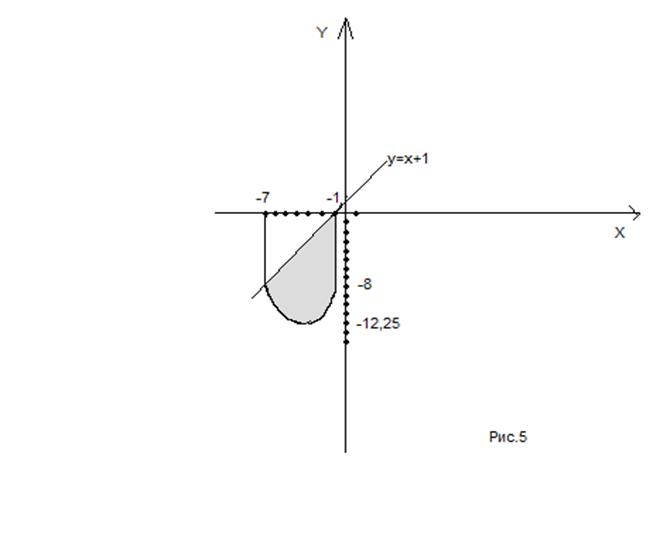
Искомая площадь фигуры согласно по формуле (5) такова:

Ответ:Площадь искомой фигуры равна .

Задачи 61-70

Для решения задач 61-70 необходимо изучить следующие темы:

1. Дифференциальные уравнения (общие понятия) [2] гл. XIII §2

2. Дифференциальные уравнения первого порядка [2] гл. XIII §3

3. Уравнения с разделяющимися переменными [2] гл. XIII §4

4. Однородные уравнения первого порядка [2] гл. XIII §5

5. Линейные уравнения первого порядка [2] гл. XIII §2

Указанные разделы учебников содержат следующие основные теоретические сведения

Дата добавления: 2015-07-25