Интегрирование рациональных дробей

7.1. Многочленом степени n называется выражение вида:

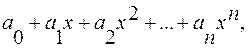где действительные числа,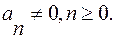

Например, - многочлен первой степени; -многочлен четвертой степени и т.д.

7.2. Многочлены в общем виде:

;

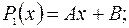
7.3. Рациональной дробью называется отношение двух многочленов:

где и 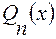- многочлены m-й и n-й степени. Будем предполагать, что эти многочлены не имеют общих корней.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.

7.4. Если рациональная дробь неправильная, то при делении ее числителя на знаменатель она представляется в виде суммы многочлена и правильной рациональной дроби.

7.5. Простейшие дроби и их интегрирование.

Простейшими (элементарными) дробями называют правильные рациональные дроби вида:

1.

2. m - целое положительное число

3. где т.е. квадратный трехчлен не

имеет действительных корней;

4. где m – целое положительное число,

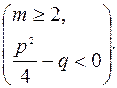
Во всех четырех случаях предполагается, что А, В, р, q- действительные числа. Перечисленные дроби будем соответственно называть простейшими дробями 1, 2, 3, 4-го типов.

Рассмотрим интегралы от простейших дробей. Имеем:

1.

2.

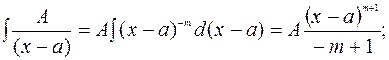
3.

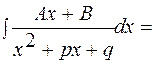
4. Вычислить интегралы не будем, если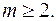

Рассмотрим частный случай простейшей дроби 3-го типа:

7.6. Любая правильная рациональная дробь 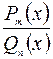может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде всего знаменатель 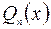записывают в виде произведения сомножителей, каждый из которых является либо степенью линейной функции 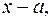либо степенью квадратной функции не имеющей действительных корней. После этого приступают к нахождению простейших дробей, составляющих в сумме данную дробь .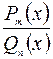

Знаменателями таких простейших дробей могут быть линейные и квадратичные множители, входящие в разложение, причем в степенях не больших, чем те, в которых они входят в это разложение. Поэтому каждому сомножителю 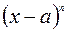разложения 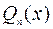отвечает в разложении дроби 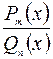выражение вида:

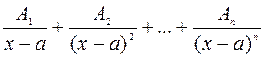(21)

В частности, при :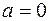

А каждому сомножителю – выражение вида:

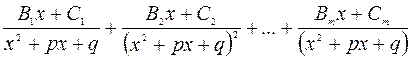(22)

7.7. Пусть знаменатель правильной дроби разлагается на множители 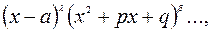(23)

где а- действительный корень кратности λ,

– квадратный трёхчлен с отрицательным дискриминантом (при этом множители со степенью , отсутствуют. Тогда правильная дробь разлагается на сумму простейших дробей следующим образом:

(24)
где коэффициенты

Определяются в процессе разложения правильной дроби.

Выражение (24)называется разложением правильной дроби на простейшие дроби.

Равенство (24) имеет место для всех 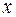, не являющихся вещественными корнями многочлена .

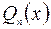Отсюда получаем следующее практическое правило разложения правильной рациональной дроби 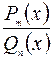на простейшие дроби.

1) Разложить знаменатель дроби на линейные и квадратичные множители, не имеющие действительных корней, используя формулы:

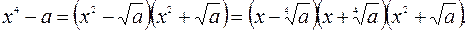
2) Записать разложение данной рациональной дроби 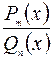в сумму простейших дробей с неопределенными (буквенными) коэффициентами, используя выражения (21) и (22).

3) Полученную сумму простейших дробей приводим к общему знаменателю и получаем дробь с неопределенными коэффициентами. Чтобы ее найти, нужно помнить:

а) дроби равны, если равны соответственно их числители и знаменатели;

б) многочлены равны, если равны коэффициенты при одинаковых степенях неизвестного.

4) Определение коэффициентов разложения (24) рациональной дроби на простейшие дроби (метод неопределенных коэффициентов).

Чтобы определить числа умножим обе части разложения (24) с неизвестными пока коэффициентами на .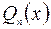

Посколько равенство между многочленом и многочленом, который получится в правой части, должно быть справедливо для всех 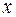, то коэффициенты, стоящие при равных степенях, должны быть равны между собой. Приравнивая их, получаем систему уравнений первой степени, из которой найдем неизвестные числа Такой метод нахождения коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов.

Можно также определить эти коэффициенты, полагая в равенстве (5) или ему эквивалентном 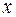равным подходяще подобранным числам (в первую очередь значениям действительных корней знаменателя ).

5) Решить полученную систему линейных уравнений относительно искомых коэффициентов.

Проиллюстрируем вышеизложенное решением простейших задач.

Дата добавления: 2015-07-25