Интегрирование f(t).

и ,

то есть дифференцирование и интегрирование f (t) соответствует соответственно умножению и делению изображения на p.

Теорема смещения. F (p+l)Ì f (t).

Теорема запаздывания. e^-λpF (p)Ì f (t–l) ¡ (t–l), где ¡ (t–l) – единичная ступенчатая функция. Если f (t) =¡ (t – l), то ее изображение для запаздывания l будет ¡ (t-l).

Теорема разложения Хевисайда. Теория разложения рациональных функций на простые дроби показывает, что если знаменатель P (p) – полином m -й степени c только простыми корнями a_n, а числитель Q (p) – любой полином более низкой степени, то имеет место тождество

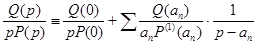
(суммирование по n от 1 до m).

Так как , то для функции f (t), оригинал которой соответствует изображению , получим:

f (t) = .

Если f (t)É , то только для простых корней

f (t) = .

Для случая кратных корней формула имеет более сложный вид:

, где . (*)

r – количество разных корней, n_k – кратность k -го корня, k – текущий номер корня, j – текущая кратность.

Дата добавления: 2015-07-25