Общие сведения. Мы уже отмечали, что наиболее просто вычисляются решения линейных дифференциальных

Мы уже отмечали, что наиболее просто вычисляются решения линейных дифференциальных уравнений; для линейного уравнения первого порядка это решение – экспонента, для уравнения n -го порядка – сумма экспонент. Этот тип дифференциальных уравнений и описываемых с их помощью линейных (или искусственно линеаризованных для упрощения) систем широко используется на практике при решении всех перечисленных классов задач – идентификации, анализа и управления.

Еще в конце 19-го века английский физик О. Хевисайд предложил способ вычислений, который назвал операционным. Он рассматривал знак дифференцирования d / dt как оператор р и операцию дифференцирования записывал как pf (t), n -я производная записывалась как pⁿf (t) – то есть оператор p n раз прилагался к функции f (t). Оператор 1/ p или
р ^-1 представлял операцию интегрирования, так как приложение оператора р к р ^-1 снова давало f (t): pp ^-1 f (t) =f (t). При этом формулы с дифференциалами и интегралами приводились к алгебраической форме – Хевисайд называл это алгебраизацией задачи. До работ Карсона и Леви, давших методу фундаментальное математическое основание, обращаться с оператором р как с алгебраическим числом в вычислениях было небезопасно – в этом приеме скрывалось множество скрытых ловушек и только гениальная интуиция Хевисайда спасала его от ошибок в вычислениях.

Современное операционное исчисление рассматривает либо функции, связанные интегральным преобразованием Карсона

F_K (p) =р ,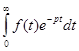

либо преобразованием Лапласа:

F_L (p) = .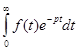

В результате обоих преобразований функция f (t) вещественного переменного t преобразуется в функцию F (p) комплексного аргумента p=s+iw, (s и w – вещественные, i= ).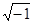

Между функциями F_K (p) и F_L (p) очевидна взаимосвязь вида

pF_L (p) =F_K (p).

Преобразование Карсона удобно использовать в анализе электрических цепей, а мы будем использовать преобразование Лапласа (опуская индекс L в обозначении) в соответствии со сложившейся практикой в большинстве прикладных областей.

Приведенное функциональное соотношение записывают в виде F (p)Ì f (t) или f (t)É F (p) и говорят, что «F (p) есть изображение f (t)» или «f (t) есть оригинал F (p)». Достаточным условием существования изображения функции f (t) является требование ее кусочной непрерывности и существования таких положительных чисел М и s, чтобы | f (t)| <Me^αt.

Рассмотрим некоторые правила операционного исчисления.

Сложение. Так как преобразование Лапласа – линейная операция, то изображение суммы равно сумме изображений 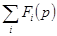Ì 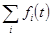. Справедливо и обратное – оригинал суммы равен сумме оригиналов.

Дифференцирование f(t). Умножим на р обе части преобразования Лапласа для f (t)и проинтегрируем по частям:

pF (p) = = + ,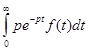

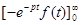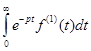то есть

pF (p)– f (0)Ì f ⁽¹⁾(t).

Если f (0) = 0, то

pF (p)Ì f ⁽¹⁾(t).

Повторив n раз тот же прием, получим последовательным интегрированием по частям

pⁿF (p)– p^{n -1} f (0)– p^{n -2} f ⁽¹⁾(0)–…– pf ^{(n -2)}(0)– f ^{(n -1)}(0)Ì f ⁽ⁿ⁾(t).

Если f (0) =f ⁽¹⁾(0) = … =f ^{(n -1)}(0), то pⁿF (p)Ì f ⁽ⁿ⁾(t).

Дата добавления: 2015-07-25