Примеры интегрирования линейных дифференциальных уравнений с постоянными коэффициентами операторным методом.

1) Дифференциальное уравнение

+ 3 y= 1

при начальных условиях при t= 0 y ₀ = 3, =– 2 дает уравнение в изображениях вида

(p ² + 4 p+ 3) Y (p) = 1 +p ² y ₀ + + 4 py ₀ = 3 p ² + 10 p+ 1,

откуда

Y (p) =

Оригинал y (t) для изображения Y (p) найдется по теореме разложения, в нашем случае корни характеристического полинома p ² + 4 p+ 3 равны p ₁ = –1, p ₂ = –3 и

.

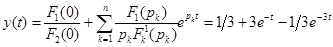2) Уравнение

dy / dt+ 3 y=e ^{–2 t}

при начальном условии y ₀ = 0 в изображениях имеет вид

(p+ 3) Y (p) =p /(p+ 2),

изображение решения

Y (p) =p /((p+ 2)(p+ 3)),

а оригинал

y (t) =e ^{–2 t} – e ^{–3 t} .

3) Дифференциальное уравнение

с начальными условиями y ₀ = 0, = 0 в изображениях имеет вид

(p ² + 2 p+ 2) Y (p) = ,

изображение решения

Y (p) = ,

корни характеристического полинома p ₁ =i, p ₂ = – i, p ₃ = –1 +i, p ₄ = –1– i и по теореме разложения

y (t) =

после некоторых преобразований получаем

y (t) = .

Дата добавления: 2015-07-25