Введение в теорию устойчивости линейных стационарных систем авторегулирования

Реакция линейной системы на управляющее или возмущающее воздействие всегда состоит из двух составляющих – собственного и вынужденного движения. Если входные функции имеют дробно-рациональные изображения, то

x_своб (t) = 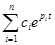, x_вын (t) =

где p_i – полюсы передаточной функции (или нули характеристического полинома), p_k – полюсы изображения воздействия.

Система автоматического регулирования может нормально функционировать только в том случае, если собственные или свободные движения, возникающие в силу различных причин, с течением времени затухают до нуля; если система удовлетворяет этому условию, то ее называют устойчивой. Если собственное движение системы расходится, то система неустойчива. Собственное движение представляет собой сумму экспоненциальных составляющих, порожденных корнями характеристического полинома – затухание или незатухание соответствующей компоненты полностью определяется значением соответствующего полюса передаточной функции – вернее, его вещественной частью. Если вещественный корень отрицателен или комплексный корень имеет отрицательную вещественную часть, то соответствующая компонента свободного движения системы затухает, положительность вещественного корня или вещественной части комплексного корня порождают расходящийся процесс. При нулевой вещественной части комплексных корней (при чисто мнимых корнях) порождается колебательная компонента с постоянной амплитудой колебаний – такая система считается находящейся на границе устойчивости. Очевидно, что достаточно одной расходящейся компоненты, чтобы система в целом потеряла устойчивость. Поэтому определение устойчивости звучит просто:

Линейная стационарная система устойчива, если все вещественные корни ее характеристического уравнения отрицательны, а все комплексные корни имеют отрицательную вещественную часть. Система, у которой хотя бы один из корней характеристического уравнения располагается левее мнимой оси – неустойчива.

Для анализа устойчивости системы в теории автоматического регулирования разработан ряд правил, позволяющих анализировать устойчивость систем без решения их характеристических уравнений – их называют критериями устойчивости. Сегодня не составляет труда с помощью компьютерной программы решить уравнение любого порядка и по его корням определить устойчивость соответствующей системы. Но значения корней ничего не говорят о причинах возможно обнаруженной неустойчивости и о том, какие параметры системы надо изменить для обеспечения устойчивости, поэтому разработанные критерии сохраняют свое значение и в настоящее время. Наиболее известные из критериев устойчивости следующие:

Критерий устойчивости Рауса-Гурвица – условия отсутствия у многочлена нулей с положительной вещественной частью формулируются в виде системы неравенств, составленных по коэффициентам многочлена. Неравенства Гурвица записываются в форме определителей (их количество равно порядку уравнения), составленных из коэффициентов многочлена по специальным правилам; доказывается, что полином не имеет нулей в правой полуплоскости, если все определители положительны.

Частотный критерий устойчивости Михайлова. Из характеристического полинома подстановкой вместо аргумента jw образуется функция комплексного аргумента A (w) e^{jj ( w )}. Критерий формулируется так: Многочлен является многочленом Гурвица (т.е. система устойчива), если полное приращение фазы при изменении частоты от нуля до бесконечности равно np/2, где n – степень полинома.

Амплитудно-фазовый критерий Найквиста. Позволяет судить об устойчивости замкнутой системы по поведению годографа амплитудно-фазовой характеристики разомкнутой и формулируется так: Замкнутая система устойчива, если полное приращение аргумента 1+W(jw) равно 2kp/2, где k – число полюсов передаточной функции разомкнутой системы W(p), находящихся справа от мнимой оси комплексной плоскости.

Дата добавления: 2015-07-25