Частотные характеристики линейных динамических систем

Эти характеристики – эффективный инструмент исследования свойств системы, позволяющий определить, как подавляются высокие или усиливаются резонансные частоты, как сдвигаются по фазе входные гармоники при прохождении через систему. Для получения частотной характеристики необходимо найти частное решение неоднородного уравнения системы при входном воздействии

u (t) =A _вх ,

где u (t) – комплексная величина, которую на комплексной плоскости можно изобразить в виде вектора, образующего с вещественной осью угол wt+j, линейно возрастающий в функции t; поэтому вектор вращается против часовой стрелки с угловой скоростью w.

Установившееся движение на выходе линейной передающей системы – гармонические колебания с частотой входных и частное решение уравнения системы ищется в форме входного воздействия, то есть f (t) =A _вых(t) – выходной вектор вращается со скоростью входного, но имеет другой модуль и смещен относительно входного на угол j=j_вых–j_вх. Подстановка указанного решения в уравнение системы и определение отношения f (t)/ u (t) =W (jw) =Q (jw)/ P (jw) приводят к комплексному коэффициенту передачи или амплитудно-фазовой характеристике системы. Запись последней формулы в показательной форме W (jw) =W (w) 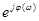, где W (w) =А _вых/ A _вх – амплитудно-частотная характеристика, j (w) =j _вых– j _вх – фазо-частотная характеристика. Так как W (jw) – дробно-рациональная функция, то амплитудно-частотная характеристика вычисляется как отношение модулей числителя и знаменателя и определяется просто: W (w) = , а фазовая характеристика как разность фазовых углов: j (w) = arctg –arctg .

Частотные характеристики элементарных звеньев.

Усилительное звено.

W (jw) =k; W (w) =k; j (w) = 0; U (w) =k; V (w) = 0.

Годограф W (jw) вырождается в точку на вещественной оси, так как при любых частотах W (jw) равно единственному значению k. Фазовый сдвиг отсутствует и все частоты входного сигнала усиливаются одинаково.

Запаздывающее звено.

W (jw) =e ^{– j} ; W (w) = 1; j (w) = – wt, то есть амплитуда на выходе равна входной, а фаза отстает от входной на угол, пропорциональный частоте. Годограф W (jw) представляет собой окружность с центром в начале координат.

Инерционное звено.

W (jw) = ; W (w) = ; φ (ω) =– arctg Tw; U (w) = ; V (w) = .

Усиление звена падает с ростом частоты – при близких к нулю частотах сигнал воспроизводится почти как у усилительного звена, а при высоких звено вообще не пропускает сигнал на выход и подавление высоких частот тем интенсивнее, чем больше постоянная времени Т. Фазовая характеристика отрицательна и выходные колебания отстают по фазе от входных, угол отставания при w ®¥ стремится к p /2. При w= 1/ T j (w) = – p /4. Годограф АФХ – окружность с радиусом с центром на вещественной оси на расстоянии k /2 от начала координат, положительным частотам соответствует нижняя полуокружность.

Колебательное звено второго порядка.

W (jw) = 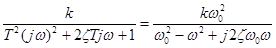; W (w) = , j (w) = –arctg U (w) = ; V (w) = .

Здесь w ₀ = 1/ T – частота собственных колебаний звена, ζ – коэффициент затухания.

Амплитудные характеристики – типичные резонансные кривые, явление резонанса лучше проявляется при малом затухании ζ при частоте, близкой к собственной w ₀. Максимум кривой W (w) наступает при частоте w_р= , величина максимума W (w_p) = , при w=w ₀; W (w ₀) =k /2 ζ.

Амплитудная (а) и фазовая (б) частотные характеристики колебательного звена при различных коэффициентах затухания ζ.

Вещественные (а) и мнимые (б) частотные характеристики колебательного звена при различных коэффициентах затухания ζ.

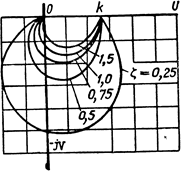
Годограф W (jw) колебательного звена при различных коэффициентах затухания ζ.

Кривая W (w) имеет максимум только при ζ< 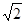/2. При ζ= 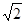/2 кривая имеет максимум при нулевой частоте, а при больших затуханиях W (w) – убывающая функция частоты. При резонансе и слабом затухании усиление во много раз больше коэффициента усиления звена и это широко используется для усиления слабых сигналов в приемных радиоустройствах. В системах авторегулирования, напротив, используют колебательные звенья с сильным затуханием в полосе частот ниже собственной.

Фазовый сдвиг между входом и выходом уменьшается с уменьшением затухания, при w=w ₀ и нулевом затухании происходит скачок фазы и при более высоких частотах сдвиг по фазе равен p.

Вещественная частотная характеристика меняет знак в точке w=w ₀.

Амплитудно-фазовая характеристика начинается на вещественной оси в точке k, годограф ее вектора захватывает 2 квадранта комплексной плоскости и при бесконечной частоте касается отрицательной вещественной полуоси. При нулевом затухании годограф вырождается в 2 полупрямые на вещественной и мнимой полуосях.

Дата добавления: 2015-07-25