
Читайте также:
|
3.1. 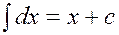
3.2. 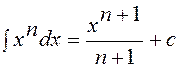
3.3. 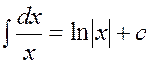
3.4. 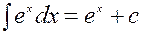
3.5. 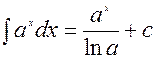
3.6. 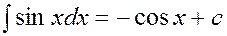
3.7. 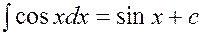
3.8. 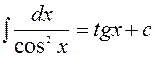
3.9. 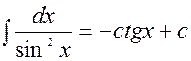
3.10. 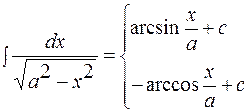
3.11. 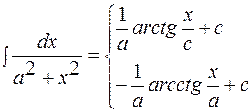
3.12. 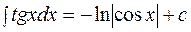
3.13. 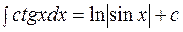
3.14. 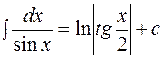
3.15. 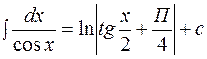
3.16. 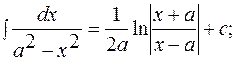
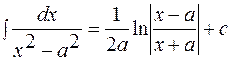
3.17. 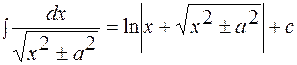
3.18. 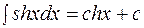
3.19. 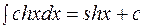
3.20. 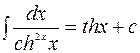
3.21. 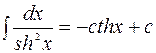
Примечание 1.
Полезно отметить часто применяемые преобразования дифференциалов, которые будем использовать при решении (a и
b – произвольные постоянные):
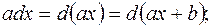
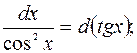
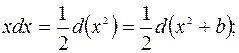
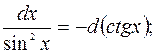
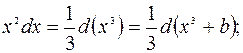
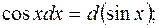
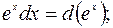
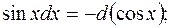
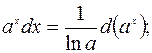
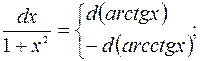
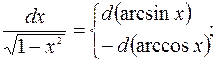
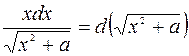
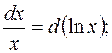
Примечание 2.
Дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной, т.е. 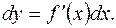
Укажем дифференциалы некоторых функций (a и b – произвольные постоянные):
1. 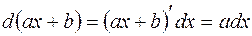
2. 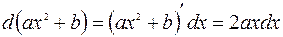
3. 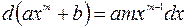
4. 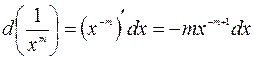
5. 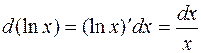
6. 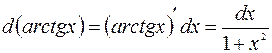
7. 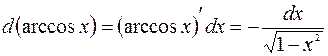
8. 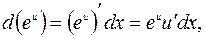 где
где 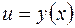
9. 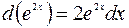
10. 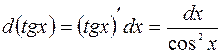
11. 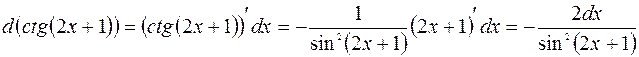
12. 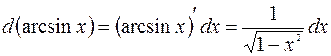
13. 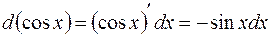
14. 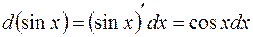
15. 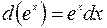
16. 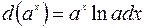
17. 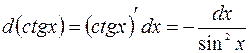
Примечание 3.
При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила:
1. Если 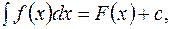 то
то 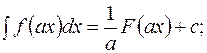
2. Если 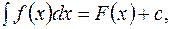 то
то 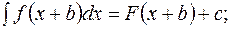
3. Если 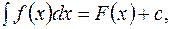 то
то 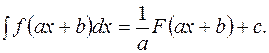
Дата добавления: 2015-07-25; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства неопределенного интеграла | | | Метод замены переменной (метод подстановки) |