Уравнение с разделяющимися перемеными.

3.1. Если дифференциальное уравнение имеет вид:

,

где коэффициент при зависит только от , а коэффициент при только от 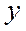, то уравнение называется уравнением с разделенными переменными.

Общее решение такого уравнения будет

3.2. Дифференциальное уравнение (30)

называется уравнением с разделяющимися переменными. Умножая обе части

данного уравнения на , получаем уравнение с разделенными переменными:

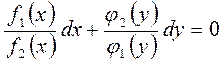
Общим интегралом этого уравнения, а следовательно, и уравнения (10), будет

3.3. Однородные дифференциальные уравнения.

Уравнение вида называется однородным, если 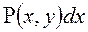и - однородные функции одного измерения.

Функция называется однородной измерения , если .

Однородное уравнение может быть приведено к виду . С помощью подстановки однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к неизвестной функции .

Дата добавления: 2015-07-25