Линейные дифференциальные уравнения первого порядка.

Уравнение вида (31)

называется линейным и входят в первых степенях, не перемножаясь между собой).

Первый способ решения

Если , уравнение называется однородным. Уравнение, в котором - неоднородным.

Общее решение уравнения 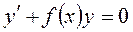легко получается разделением переменных:

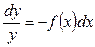; ; или ,

где 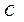- произвольная постоянная.

Общее решение линейного неоднородного уравнения находится исходя из общего решения соответствующего однородного уравнения, варьируя произвольную постоянную, т.е. полагая

где 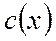- некоторая, подлежащая определению, дифференцируемая функция от .

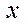Для нахождения нужно подставить в исходное уравнение, что приводит к уравнению .

Отсюда

И искомое общее решение линейного неоднородного уравнения имеет вид:

.

Второй способ решения

Линейное уравнение первого порядка можно интегрировать и введя замену , где и две неизвестные функции. Преобразуем уравнение (28), подставив в него значения и .

Получим

или

.

Одна из неизвестных функций (например ) может быть выбрана произвольно (поскольку лишь произведение должно удовлетворять уравнению (31)), принимают за любое частное решение уравнения , обращающее в нуль коэффициент при в последнем уравнении.

Т.е. ; ; ;

Тогда предыдущее уравнение примет вид:

; ; ; ;

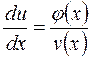Умножая на получим решение исходного уравнения:

; .

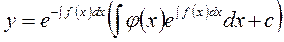Решение типового примера

Пример: Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию при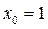

Решение: Соответствующее однородное уравнение

Найдем его общее решение:

. Имеем 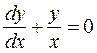или . Тогда

Отсюда . .

Ищем решение исходного неоднородного уравнения в виде ,

где - неизвестная функция.

Подставляя в исходное уравнение и , придем к уравнению или ; .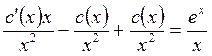

Откуда , ,

Общее решение данного уравнения .

Используя начальное условие , , получим ;

откуда

Следовательно, искомое частное решение имеет вид .

Второй способ решения

Разделим на обе части исходного уравнения: .

Для решения этого уравнения применим подстановку , тогда .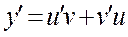

Уравнение примет вид или .

Полагая , найдем функцию , когда

; ; ; ; ;

; ; .

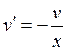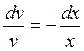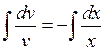Функцию найдем из условия:

Подставим , получим: , .

Отсюда находим ; ; ;

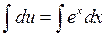и, следовательно, общее решение исходного уравнения получим в виде:

; . (*)

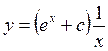Найдем частное решение, удовлетворяющее начальному условию

при .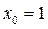

Подставим в равенство (*) и найдем .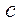

,

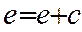Следовательно, искомое частное решение имеет вид: .

Задачи 71-80

Для решения задач 71-80 необходимо изучить следующие темы:

1. Линейные однородные уравнения 2-го порядка с постоянными коэффициентами. [2] гл. XIII §

2. Линейные неоднородные уравнения 2-го порядка с постоянными коэффициентами. 2] гл. XIII §

Указанные разделы учебников содержат следующие основные теоретические сведения

Дата добавления: 2015-07-25