Читайте также:
|
1.1. Дифференциальным уравнением называется уравнение, содержащее независимую переменную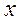 
, неизвестную функцию 
и ее производные 
, 
, …, 
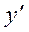1.2. Уравнение называется обыкновенным, если независимая переменная одна.
1.3. Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.
1.4. Решением дифференциального уравнения называется функция
, которая при подстановке в уравнение вместо неизвестной функции обращает его тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.
Дата добавления: 2015-07-25; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные теоретические знания | | | Дифференциальные уравнения первого порядка. |