Граничные условия уравнения Лапласа для однородной изотропной среды.

Для однородной среды (σ = 1/r = const) уравнение 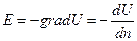преобразуется в дифференциальное уравнение Лапласа div (σ grad U) = Δ U = 0 или в прямоугольной системе координат в формулу d²U/dx² + d²U/dt² + d²U/dz² =0, решение которой дает возможность найти функцию U как функцию координат исследуемой точки М.

Функция U должна удовлетворять следующим граничным условиям:
1. Вблизи от источника тока А, с которым совмещается начало координат, потенциальная функция U должна стремиться к выражению потенциалов в однородной и изотропной среде, т. е. при R = sqr(x²+y²+z²) → 0, U → Ir / 4pR.

2. В бесконечно удаленных точках U → 0.

3. В точках, бесконечно близко расположенных к поверхности S, ограничивающей любую область v_i удельного электрического сопротивления отокружающего пространства v_e удельного сопротивления и разделенных этой поверхностью, потенциальные функции U_i (в области v_i)и U_е (в области v_e), согласно условию непрерывности потенциала, должны быть равными друг другу, т.е. на поверхности S: (U_i)_s = (U_e)_s.

4. На этой же поверхности S должно соблюдаться постоянство нормальной составляющей плотности тока (1/r_i)*(dU_i/dn) = (1/r_e)*(dU_e/dn).

Дата добавления: 2015-07-20