Читайте также:
|
Существуют следующие два варианта этого метода:
а) Метод подведения под знак дифференциала.
Пусть требуется вычислить интеграл 
Предположим, что существуют дифференцируемая функция 
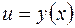и функция 
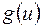такие, что подынтегральное выражение 
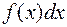может быть записано в виде 
(указанное преобразование называется подведением 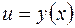под знак дифференциала). Заметим, что выполняется соотношение 
(*), где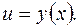 
Поэтому вычисление интеграла (*) сводится к вычислению интеграла 
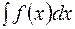(который может оказаться проще исходного) и следующей подстановке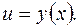
б) Метод подстановки.
Этот метод состоит в том, что 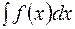иногда можно упростить путем введения вместо 
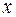какой-либо новой переменной. При помощи надлежащего выбора новой переменной удается привести некоторые интегралы к более простому виду, после чего их вычисляют.
Пусть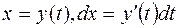 
В этом случае имеет место формула:
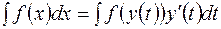
Итак, для преобразования неопределенного интеграла 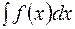к новой переменной 
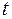, полагая 
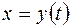, достаточно преобразовать к новой переменной его подынтегральное выражение.
Вместо подстановки 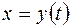иногда употребляют и обратную подстановку: 
Дата добавления: 2015-07-25; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные формулы интегрирования | | | Интегрирование по частям. |