Решение типовых примеров.

1. Непосредственное интегрирование

Найти следующие интегралы:

1.

На основании свойства (2.4) постоянный множитель выносим за знак интеграла, а используя формулу (3.1), получим

2.

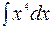
По формуле (3.2) имеем

3.

По формуле (3.2) имеем

4.

Используя свойство (2.4) и формулу (3.2), имеем

5.

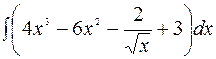
Используя свойство (2.4) и формулы (3.1) и (3.2), имеем

6.

По формуле (3.3) находим

7.

По формуле (3.5) при а=2 получим

8.

По формуле (3.5) при имеем

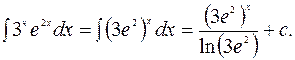
9.

По формуле (3.11) при получим .

10.

Используя свойства (2.4) и (2.5) и формулы (3.1), (3.6), (3.7), имеем

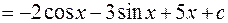
11.

Используя свойства (2.4) и (2.5) и формулы (3.2) и (3.4), имеем

12.

Используя свойства (2.4) и (2.5) и формулу (3.8) и (3.9), получим

13.

Возведя в квадрат и используя свойства (2.4) и (2.5), находим

Воспользуемся тригонометрическими формулами

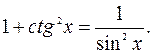
подставим их в интегралы, получим

По формулам (3.8), (3.9), (3.1)

14.

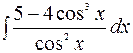
Воспользуемся свойствами (2.4) и (2.5) и, применяя формулу (3.8) и (3.7), находим

15.

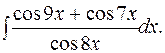
Используя тригонометрическую формулу 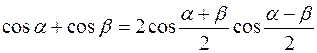и формулу (3.7), получим

16.

По формуле (3.16) находим

17.

По формуле (3.17) имеем

.

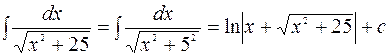2. Метод замены переменной

Метод подведения под знак дифференциала.

1.

Данный интеграл окажется табличным, если под знаком дифференциала будет стоять аргумент т.е. , то по формуле (3.2)

2.

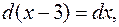Интеграл будет табличным, если под знаком дифференциала будет стоять аргумент . Так как то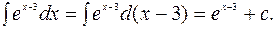

3.

Так как , то

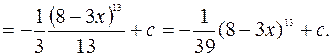
4.

Так как (3.12) имеем

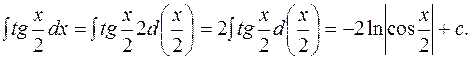
5.

Так как то , и по формуле (3.7) имеем

6.

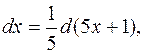Так как то и по формуле (3.4)

7.

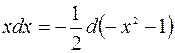Так как и то по формуле

(3.4) имеем

8.

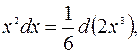Так как и то по формуле (3.5)

находим

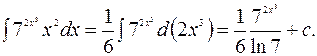
9.

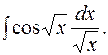
Так как и , то по формуле (3.7)

находим

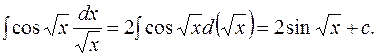
10.

Так как и , то по формуле (3.4)

получим

11.

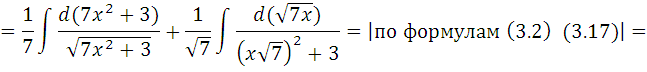
12.

Так как и то по формуле (3.15) находим

3. Интегрирование по частям

(20)

1. Найти

Решение. Положим тогда . Когда применяют интегрирование по частям – по находят , то произвольной постоянной не вводят, из множества первообразных функций для берут какую-нибудь одну, наиболее удобную. Подставив в формулу (20) найденные выражения, получим

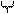
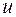
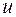
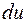
Замечание. При вычислении этого интеграла нецелесообразно брать так как в этом случае было бы 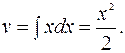Применяя формулу (20), мы получили бы Совершенно очевидно, что интеграл в правой части сложнее исходного. Из этого делаем вывод, что выбор 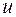и не может быть произвольным. Он определяется требованием, чтобы интеграл, к которому приводит формула (20), был проще заданного.

2. Найти

Решение. Положим 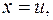тогда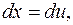

Подставив в формулу (20) найденные выражения, получим

Замечание. Если бы выражение 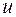и мы выбрали иначе, например, откуда и пришли бы к интегралу более сложному, чем исходный, так как степень сомножителя при тригонометрической функции повысилась на единицу.

3. Найти

Решение. Положим тогда

Подставим найденные выражения в формулу (20), получим

4. Найти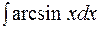

Решение. Положим 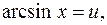тогда , Подставим найденные выражения в формулу (20) и получим

Последний интеграл найдем отдельно:

Примечание.

Получаем .

5. Найти

Решение. Полагая найдем

Следовательно, по формуле (20) имеем

6. Найти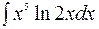

Решение. Пусть тогда

По формуле (20) имеем

4. Интегрирование рациональных дробей.

1. Выделить целую часть дроби

2. Выделить целую часть дроби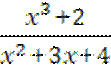

Таким образом,

3. Найти интегралы:

1)

2)

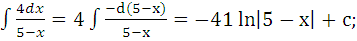
3)

4)

5)

6)

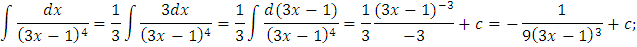
7)

Выделим полный квадрат из квадратного трехчлена, стоящего в знаменателе. Имеем

Введем замену переменных x+2=t, x=t -2, dx=dt, тогда

8)

9) Разложить на простейшие дроби рациональную дробь

Дробь правильная, тогда запишем:

Дроби равны, если

(**)

Найдем корни знаменателя:

Подставим значения корней знаменателя в тождество (**).

Получим:

a) x=0, 4=

б) x=2, 4+4-4=

в) x= 3, 9-6-4=

Получим

10) Найти интеграл

Дробь неправильная, старшая степень многочлена числителя больше старшей степени многочлена знаменателя.

а) Выделим целую часть дроби:

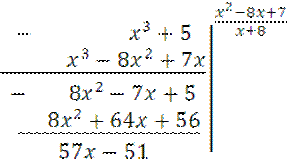
Получаем

б) Разложим знаменатель дроби на простые множители:

+7=0;

+7=(x-1)(x-7);

в) Запишем правильную дробь в виде суммы простейших дробей с неопределенными коэффициентами и найдем их:

. (***)

Подставим в тождество (***) значения корней знаменателя.

Получим:

x=1, 57

x=7, 57

Тогда имеем

Таким образом,

=

=

=

=

Ответ:

ЗАДАЧИ 51-60.

Для решения задач 51-60 надо изучить вычисление площади плоской фигуры [2],T.1,гл.13,§1.

Указанный раздел учебника содержит следующие основные теоретические сведения.

---

Дата добавления: 2015-07-25