Читайте также:
|
2.1. 
т.е. производная от неопределенного интеграла равна подынтегральной функции.
2.2.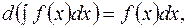 
т.е. дифференциал неопределенного интеграла равен подынтегральному выражению.
2.3. 
т.е. неопределенный интеграл от дифференциала любой функции равен этой функции плюс произвольная постоянная.
2.4.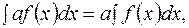 
где а – постоянная, т.е. постоянный множитель можно выносить за знак интеграла.
2.5. 
т.е. интеграл алгебраической суммы конечного числа функции равен алгебраической сумме неопределенных интегралов этих функций.
2.6. Если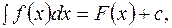 
т.е. всякая формула
то и 
где 
интегрирования сохраняет
- любая дифференцируемая свой вид при подстановке
функция от x, вместо независимой
переменной любой
дифференцируемой
функции от неё.
Дата добавления: 2015-07-25; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ВВЕДЕНИЕ | | | Основные формулы интегрирования |