ВВЕДЕНИЕ. Математический анализ

Математический анализ

Методические указания, образцы выполнения и задания

контрольных работ

для студентов заочной, очно-заочной форм обучения направлений подготовки

«Экономика», «Менеджмент»

Калининград

ВВЕДЕНИЕ

В процессе изучения математических курсов студент должен выполнить ряд контрольных работ. В данных методических указаниях даны основные теоретические сведения, образцы выполнения контрольной работы №3.

Задачи 41-50

Для решения задач 41-50 надо изучить следующий материал:

1. Первообразная и неопределённый интеграл [2], т.1, гл. X.

2. Основные свойства неопределенного интеграла [2], т.1, гл. X.

3. Основные формулы интегрирования [2], т.1, гл. X.

4. Непосредственное интегрирование [2], т.1, гл. X.

5. Метод замены переменной [2], т.1, гл. X.

6. Интегрирование по частям [2], т.1, гл. X.

7. Интегрирование рациональных дробей [2], т.1, гл. X.

Указанные разделы учебников содержат следующие основные теоретические сведения.

1. Первообразная и неопределенный интеграл

1.1. Во многих теоретических и прикладных вопросах математического анализа приходится решать задачу, обратную дифференцированию, а именно: по заданной производной или, что то же, по заданному дифференциалу , найти первоначальную функцию, так называемую первообразную функцию 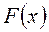.Действие нахождения первообразных функций называется интегрированием функций. Функция 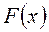называется первообразной для данной функции на отрезке [a, b, ], если во всех точках этого отрезка выполняется равенство или, что то же, . Если функция имеет первообразную , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 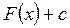, где с – произвольная постоянная. Если функция 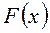является первообразной для , то выражение называется неопределенным интегралом и обозначается символом . Таким образом, по определению , если 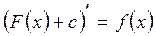. При этом функцию называют подынтегральной функцией, – подынтегральным выражением, –переменной интегрирования, знак – знаком интеграла. Геометрически в системе координат графики всех первообразных функций от данной функции представляют семейство кривых, зависящее от данного параметра , которые получаются из другой путем параллельного сдвига вдоль оси (рис.1.

	Рис. 1

Рис 5.

Дата добавления: 2015-07-25