
Читайте также:
|
2.1. Уравнение вида  или
или 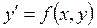 (27)
(27)
называется дифференциальным уравнением первого порядка.
2.2. Задача Коши. Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнени  задача Коши ставится следующим образом:
задача Коши ставится следующим образом:
среди всех решений уравнения (27) найти такое решение  , (28)
, (28)
в котором функция  принимает заданное числовое значение
принимает заданное числовое значение  при заданном числовом значении
при заданном числовом значении 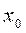 независимой переменной
независимой переменной  ,
,
т.е.  (29)
(29)
где 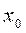 и
и  заданные числа, так что решение (28) удовлетворяет условиям:
заданные числа, так что решение (28) удовлетворяет условиям: 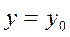 при
при 
Условия  при
при  (другая запись
(другая запись  ) называются начальными условиями этого решения.
) называются начальными условиями этого решения.
2.3. Общим решением дифференциального уравнения первого порядка  в области
в области 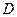 называется функция обладающая следующими свойствами:
называется функция обладающая следующими свойствами:
1) она является решением данного уравнения при любых значениях производной постоянной  , принадлежащих некоторому множеству;
, принадлежащих некоторому множеству;
2) для любого начального условия  такого, что
такого, что 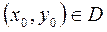 , существует единственное значение
, существует единственное значение  , при котором решение
, при котором решение  удовлетворяет заданному начальному условию.
удовлетворяет заданному начальному условию.
Если общее решение уравнения (27) задано в неявном виде 
или  , то оно называется общим интегралом этого уравнения.
, то оно называется общим интегралом этого уравнения.
Дата добавления: 2015-07-25; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дифференциальные уравнения (общие понятия). | | | Уравнение с разделяющимися перемеными. |