Линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами.

2.1. Линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами, т.е. уравнение с правой частью, записывается в следующем виде:

2.2. Общее решение линейного неоднородного уравнения равно сумме любого его частного решения 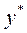и общего решения соответствующего однородного уравнения , т.е.

2.3. Частное решение 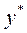уравнения

надо искать в виде:

Во всех случаях за надо взять многочлен с буквенными коэффициентами, которые находятся после подстановки 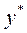в уравнение методом неопределенных коэффициентов.

2.4. Частное решение 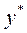уравнения

надо искать в виде:

Во всех случаях за надо взять многочлен с буквенными коэффициентами, которые определяться после подстановки 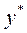в уравнение методом неопределенных коэффициентов.

2.5. Частное решение 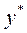уравнения

надо искать в виде:

, если не корень характеристического уравнения; , если корень характеристического уравнения.

Дата добавления: 2015-07-25