Пример 1. Найти общее решение дифференциального уравнения

Найти общее решение дифференциального уравнения

и частное решение, удовлетворяющее начальным условиям:

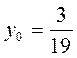, при

а) Найдем общее решение однородного уравнения

Характеристическое уравнение имеет два

равных корня . Тогда общее решение (второй вид):

б) Функцию 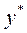- частное решение данного уравнения найдем методом неопределенных коэффициентов по виду правой части (пункт 2.4)

В нашем примере

Следовательно, , так как

Дифференцируя 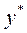два раза и подставляя производные в данное уравнение, получим:

; ; ; ; .

Таким образом, , а общее решение данного уравнения

есть (34)

в) Найдем частное решение, удовлетворяющее начальным условиям:

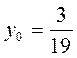; при

Продифференцируем общее решение (34) и получим:

,

(35)

Полагая , при , и получим систему уравнений (31) и (32) относительно неизвестных , и решим ее:

;

; ;

Следовательно, искомое частное решение имеет вид:

.

Дата добавления: 2015-07-25