
Читайте также:
|
Задача №1.Вычислить неопределенные интегралы:
Вариант 1.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 2.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 3.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 4.
а)  ; б)
; б) 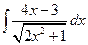 ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 5.
а)  ; б)
; б)  ; в)
; в) 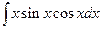 ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 6.
а)  ; б)
; б) 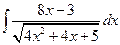 ; в)
; в) 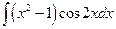 ;
;
г)  ; д)
; д) 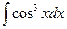 ; е)
; е)  .
.
Вариант 7.
а)  ; б)
; б)  ; в)
; в) 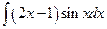 ;
;
г)  ; д)
; д)  ; е)
; е) 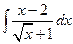 .
.
Вариант 8.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 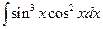 ; е)
; е)  .
.
Вариант 9.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Вариант 10.
а) 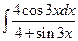 ; б)
; б)  ; в)
; в)  ;
;
г) 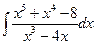 ; д)
; д)  ; е)
; е) 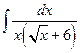 .
.
Задача 2. Приложения определенного интеграла: а) вычислить площадь плоской фигуры, ограниченной линиями; б) вычислить длину дуги плоской кривой; в) найти объем тела, полученного вращением фигуры, ограниченной линиями.
Вариант 1.
а)  б)
б)  в)
в)  .
.
Вариант 2.
а)  б)
б)  в)
в) 
Вариант 3.
а)  б)
б)  в)
в) 
Вариант 4.
а)  б)
б)  в)
в) 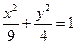 .
.
Вариант 5.
а) 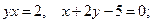 б)
б)  ; в)
; в) 
Вариант 6.
а)  б)
б) 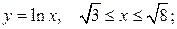 в)
в) 
Вариант 7.
а) 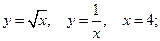 б)
б) 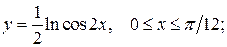 в)
в) 
Вариант 8.
а)  б)
б)  в)
в) 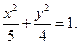
Вариант 9.
а)  б)
б)  в)
в) 
Вариант 10.
а) 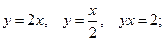 б)
б)  в)
в) 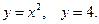
Дата добавления: 2015-07-25; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Неопределенный интеграл. | | | Задача 3. Дифференциальные уравнения с разделяющимися переменными. Найти общее решение. |